题目内容
【题目】如图，已知抛物线y=﹣x2+mx+3与x轴交于点A、B两点，与y轴交于C点，点B的坐标为（3，0），抛物线与直线y=﹣
x+3交于C、D两点．连接BD、AD．
（1）求m的值．
（2）抛物线上有一点P，满足S△ABP=4S△ABD，求点P的坐标．
【答案】（1）2；（2）P（1+
，-9）或P（1-
，-9）．
【解析】试题分析：（1）利用待定系数法即可解决问题；
（2）利用方程组首先求出点D坐标．由面积关系，推出点P的纵坐标，再利用待定系数法求出点P的坐标即可.
试题解析：（1）∵抛物线y=-x2+mx+3过（3，0），
∴0=-9+3m+3，
∴m=2
（2）由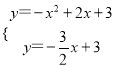
，得
， 
，
∴D（
，-
），
∵S△ABP=4S△ABD，
∴
AB×|yP|=4×
AB×
，
∴|yP|=9，yP=±9，
当y=9时，-x2+2x+3=9，无实数解，
当y=-9时，-x2+2x+3=-9，解得：x1=1+
，x2=1-
，
∴P（1+
，-9）或P（1-
，-9）．
练习册系列答案
相关题目
【题目】在某校开展的“书香校园”读书活动中，学校为了解八年级学生的读书情况，随机调查了八年级50名学生每学期每人读书的册数，绘制统计表如下：
册数 | 0 | 1 | 2 | 3 | 4 |
人数 | 4 | 12 | 16 | 17 | 1 |
则这50个样本数据的众数和中位数分别是（ ）
A.17，16
B.3，2.5
C.2，3
D.3，2