Question

【题目】如图，直线l1与直线交于点，直线l1分别交x轴、y轴于点A,B，OB=2，直线l2交x轴于点C.

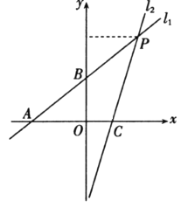
（1）求m的值及四边形OBPC的面积;

（2）求直线l1的解析式;

（3）设点Q是直线l2上的一动点，当以A、C、Q为顶点的三角形的面积等于四边形OBPC的面积时，求点Q的坐标.

Answer 1

【答案】（1）m＝2，四边形OBPC的面积的面积为4；（2）y1=x+2；（3）点Q的坐标为（，）或（，）.

【解析】

（1）把P（m，4）代入y2＝4x4可求出m＝2，则P点坐标为（2，4），然后根据B点坐标为（0，2）求出直线l1解析式，进而得到A、C的坐标，然后根据四边形OBPC的面积＝S△APC－S△ABO进行计算即可；

（2）由（1）可得直线l1的解析式；

（3）根据以A、C、Q为顶点的三角形的面积等于四边形OBPC的面积列出方程，求出Q点的纵坐标，即可解决问题.

解：（1）把P（m，4）代入y2＝4x4得4m4＝4，解得m＝2，

∴P点坐标为（2，4），

由题意得，B点坐标为（0，2），

设直线l1解析式为：y1=kx+b(k≠0)，

则，解得：，

∴直线l1解析式为：y1=x+2，

当y1=x+2=0时，解得：x=－2，即A（－2，0），

当时，解得：x=1，即C（1，0），

∴四边形OBPC的面积＝S△APC－S△ABO＝；

（2）由（1）可得，直线l1解析式为：y1=x+2；

（3）设点Q的纵坐标为（n，m），

由题意得：，即，

解得：，

当时，代入得，即Q（，），

当时，代入得，即Q（，），

综上所示：点Q的坐标为（，）或（，）.