Question

【题目】如图，中，，，，以斜边的中点为旋转中心，把这个三角形按逆时针方向旋转得到，则旋转后两个直角三角形重叠部分的面积为（ ）

A. B. C. D.

Answer 1

【答案】B

【解析】

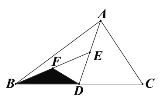
如图，先计算出AB=2AC=12，根据中点定义则可得BD=6，根据旋转的性质可得D=BD=6，在Rt△BDM中，可求得DM、BM的长，从而可求得B′M的长，然后在Rt△B′MN中求出MN的长，继而求得BN的长，在Rt△BNG中求出BN的长，然后利用S阴影=S△BNG-S△BMD进行计算即可得.

如图，∵∠C=90°，∠A=60°，AC=6，

∴AB=2AC=12，∠B=30°，

∵点D为AB的中点，

∴BD=6，

∵△ABC绕点D按逆时针方向旋转得到，

∴D=BD=6，

在Rt△BDM中，∠B=30°，∠BDM=90°，

∴BM=2DM，BD2+DM2=BM2，

∴DM=，BM=4，

∴B′M=B′D-DM=6-，

在Rt△B′MN中，∠B′=30°，

∴MN=B′M=3-，

∴BN=BM+MN=3+3，

在Rt△BNG中，BG=2NG，BG2=NG2+BN2，

∴NG=3+，

∴S阴影=S△BNG-S△BMD==9，

故选B.