题目内容
如图,已知O(0,0)、A(4,0)、B(4,3).动点P从O点出发,以每秒3个单位的速度,沿△OAB的边0A、AB、B0作匀速运动;动直线l从AB位置出发,以每秒1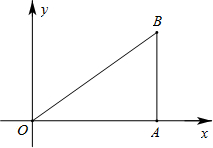 个单位的速度向x轴负方向作匀速平移运动.若它们同时出发,运动的时间为t秒,当点P运动到O时,它们都停止运动.
个单位的速度向x轴负方向作匀速平移运动.若它们同时出发,运动的时间为t秒,当点P运动到O时,它们都停止运动.(1)当P在线段OA上运动时,求直线l与以P为圆心、1为半径的圆相交时t的取值范围;
(2)当P在线段AB上运动时,设直线l分别与OA、OB交于C、D,试问:四边形CPBD是否可能为菱形?若能,求出此时t的值;若不能,请说明理由,并说明如何改变直线l的出发时间,使得四边形CPBD会是菱形.
分析:(1)根据点P与直线l的距离d<1分为点P在直线l的左边和右边,分别表示距离,列不等式组求范围;
(2)四边形CPBD不可能为菱形.依题意可得AC=t,OC=4-t,PA=3t-4,PB=7-3t,由CD∥AB,利用相似比表示CD,由菱形的性质得CD=PB可求t的值,又当四边形CPBD为菱形时,PC=PB=7-3t,把t代入PA2+AC2,PC2中,看结果是否相等如果结果不相等,就不能构成菱形.设直线l比P点迟a秒出发,则AC=t-a,OC=4-t+a,再利用平行线表示CD,根据CD=PB,PC∥OB,得相似比,分别表示t,列方程求a即可.
(2)四边形CPBD不可能为菱形.依题意可得AC=t,OC=4-t,PA=3t-4,PB=7-3t,由CD∥AB,利用相似比表示CD,由菱形的性质得CD=PB可求t的值,又当四边形CPBD为菱形时,PC=PB=7-3t,把t代入PA2+AC2,PC2中,看结果是否相等如果结果不相等,就不能构成菱形.设直线l比P点迟a秒出发,则AC=t-a,OC=4-t+a,再利用平行线表示CD,根据CD=PB,PC∥OB,得相似比,分别表示t,列方程求a即可.
解答: 解:(1)当P在线段OA上运动时,OP=3t,AC=t,
解:(1)当P在线段OA上运动时,OP=3t,AC=t,
⊙P与直线l相交时,
,
解得
<t<
;
(2)四边形CPBD不可能为菱形.
依题意,得AC=t,OC=4-t,PA=3t-4,PB=7-3t,
∵CD∥AB,
∴
=
,即
=
,
解得CD=
(4-t),
由菱形的性质,得CD=PB,
即
(4-t)=7-3t,
解得t=
,
又当四边形CPBD为菱形时,PC=PB=7-3t,当t=
时,
代入PA2+AC2=(3t-4)2+t2=
,PC2=(7-3t)2=
,
∴PA2+AC2≠PC2,就不能构成菱形.
设直线l比P点迟a秒出发,则AC=t-a,OC=4-t+a,
由CD∥AB,得CD=
(4-t+a),由CD=PB,得
(4-t+a)=7-3t,
解得t=
,
PC∥OB,PC=CD,得
=
,即AB•PC=OB•AP,
3×
(4-t+a)=5×(3t-4),
解得t=
,
则
=
,
解得a=
,即直线l比P点迟
秒出发.
 解:(1)当P在线段OA上运动时,OP=3t,AC=t,
解:(1)当P在线段OA上运动时,OP=3t,AC=t,⊙P与直线l相交时,
|
解得
| 3 |
| 4 |
| 5 |
| 4 |
(2)四边形CPBD不可能为菱形.
依题意,得AC=t,OC=4-t,PA=3t-4,PB=7-3t,
∵CD∥AB,
∴
| CD |
| AB |
| OC |
| OA |
| CD |
| 3 |
| 4-t |
| 4 |
解得CD=
| 3 |
| 4 |
由菱形的性质,得CD=PB,
即
| 3 |
| 4 |
解得t=
| 16 |
| 9 |
又当四边形CPBD为菱形时,PC=PB=7-3t,当t=
| 16 |
| 9 |
代入PA2+AC2=(3t-4)2+t2=
| 400 |
| 81 |
| 25 |
| 9 |
∴PA2+AC2≠PC2,就不能构成菱形.
设直线l比P点迟a秒出发,则AC=t-a,OC=4-t+a,
由CD∥AB,得CD=
| 3 |
| 4 |
| 3 |
| 4 |

解得t=
| 16-3a |
| 9 |
PC∥OB,PC=CD,得
| PC |
| OB |
| AP |
| AB |
3×
| 3 |
| 4 |
解得t=
| 9a+116 |
| 69 |
则
| 16-3a |
| 9 |
| 9a+116 |
| 69 |
解得a=
| 5 |
| 24 |
| 5 |
| 24 |
点评:本题考查了直线与圆的关系,勾股定理的运用,菱形的性质.关键是根据菱形的性质,对边平行,邻边相等,得出相似比及边相等的等式,运用代数方法,列方程求解.

练习册系列答案
相关题目
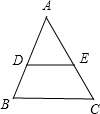 如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )
如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
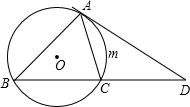 =2,∠ADC=30°
=2,∠ADC=30°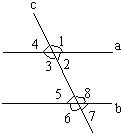 30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
 13、如图,已知直线AB∥CD,∠1=50°,则∠2=
13、如图,已知直线AB∥CD,∠1=50°,则∠2=