题目内容
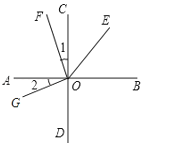
【题目】已知:如图, AB⊥CD于点O,∠1=∠2,OE平分∠BOF,∠EOB=55°,求∠GOF和∠DOG的度数.
【答案】90°;70°
【解析】
先由垂直的定义可得∠1+∠AOF=90°,再由∠1=∠2,即可求得∠GOF=90°,根据角平分线的定义可得∠BOF=2∠EOB=110°,根据平角定义可求得∠AOF=70°,继而可得∠1 =20°,再根据平角定义即可求得∠DOG的度数.
∵AB⊥CD,
∴∠AOC=90°,即∠1+∠AOF=90°,
又∵∠1=∠2,
∴∠2+∠AOF=90°,
即∠GOF=90°,
∵OE平分∠BOF,∠EOB=55°,
∴∠BOF=2∠EOB=110°,
∴∠AOF=180°-∠BOF=70°,
∴∠1=∠AOC-∠AOF=20°,
∴∠DOG=180°-∠1-∠GOF=70°.

练习册系列答案
相关题目