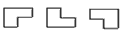题目内容
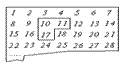
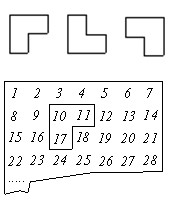 用如图所示的曲尺形框框(有三个方向),可以套住下表中的三个数,设被框住的三个数中最小的数为a.
用如图所示的曲尺形框框(有三个方向),可以套住下表中的三个数,设被框住的三个数中最小的数为a.(1)用含a的式子表示这三个数的和;
(2)若这三个数的和是48,求a的值.
分析:(1)注意三种不同的框圈住的三个数之间的大小关系,要分三种情况进行分析;
(2)根据三种不同的结果列方程求解,求得的数必须是整数,否则应舍去.
(2)根据三种不同的结果列方程求解,求得的数必须是整数,否则应舍去.
解答:解:(1)设被第一个框框住的三个数中最小的数为a,则
a+a+1+a+7=3a+8;
设被第二个框框住的三个数中最小的数为a,则
a+a+7+a+8=3a+15;
设被第三个框框住的三个数中最小的数为a,则
a+a+1+a+8=3a+9.
(2)设被第一个框框住的三个数的和是48,则
3a+8=48,解得a=
,显然和题意不合.
设被第二个框框住的三个数的和是48,则
3a+15=48,解得a=11,符合题意.
设被第三个框框住的三个数的和是48,则
3a+9=48,解得a=13,符合题意.
∴a的值为11或13.
a+a+1+a+7=3a+8;
设被第二个框框住的三个数中最小的数为a,则
a+a+7+a+8=3a+15;
设被第三个框框住的三个数中最小的数为a,则
a+a+1+a+8=3a+9.
(2)设被第一个框框住的三个数的和是48,则
3a+8=48,解得a=
| 40 |
| 3 |
设被第二个框框住的三个数的和是48,则
3a+15=48,解得a=11,符合题意.
设被第三个框框住的三个数的和是48,则
3a+9=48,解得a=13,符合题意.
∴a的值为11或13.
点评:能够正确找到圈住的三个数之间的关系.解决问题的关键是读懂题意,找到所求的量的等量关系.从所给材料中分析数据得出规律是应该具备的基本数学能力.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
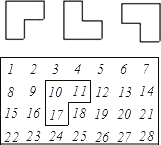 用如图所示的曲尺形框框(有三个方向),可以套住下表中的三个数,设被框住的三个数中(第一个框框住的最小的数为a、第二个框框住的最小的数为b、第三个框框住的最小的数为c).
用如图所示的曲尺形框框(有三个方向),可以套住下表中的三个数,设被框住的三个数中(第一个框框住的最小的数为a、第二个框框住的最小的数为b、第三个框框住的最小的数为c).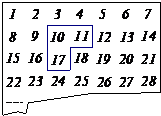 有两个如图所示的曲尺形框,框①和框②,用它们分别可以框住下表中的三个数(如图所
有两个如图所示的曲尺形框,框①和框②,用它们分别可以框住下表中的三个数(如图所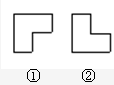 给示例),设被框住的三个数中最小的数为a.
给示例),设被框住的三个数中最小的数为a. 有两个如图所示的曲尺形框,框①和框②,用它们分别可以框住下表中的三个数(如图所
有两个如图所示的曲尺形框,框①和框②,用它们分别可以框住下表中的三个数(如图所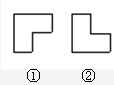 给示例),设被框住的三个数中最小的数为a.
给示例),设被框住的三个数中最小的数为a.