题目内容
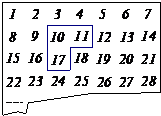 有两个如图所示的曲尺形框,框①和框②,用它们分别可以框住下表中的三个数(如图所
有两个如图所示的曲尺形框,框①和框②,用它们分别可以框住下表中的三个数(如图所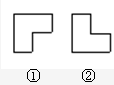 给示例),设被框住的三个数中最小的数为a.
给示例),设被框住的三个数中最小的数为a.(1)用含a的式子分别
(2)若这三个数的和是48,问a的值是否存在?若存在,求之;若不存在,说明理由.
分析:(1)根据左右相邻的2个数相邻1,上下相邻的数相差7把这3个数相加即可;
(2)分别代入(1)得到的代数式,计算即可.
(2)分别代入(1)得到的代数式,计算即可.
解答:解:(1)被①框住的三个数分别为a,a+1,a+7,∴a+a+1+a+7=3a+8,(1分)
被②框住的三个数分别为a,a+7,a+8,∴a+a+7+a+8=3a+15.(2分)
(2)当3a+8=48时,a=
.
此解不符合题意,说明a的值不存在.(4分)
当3a+15=48时,a=11.
此解符合题意.(6分)
被②框住的三个数分别为a,a+7,a+8,∴a+a+7+a+8=3a+15.(2分)
(2)当3a+8=48时,a=
| 40 |
| 3 |
此解不符合题意,说明a的值不存在.(4分)
当3a+15=48时,a=11.
此解符合题意.(6分)
点评:考查一元一次方程的应用;根据日历中相邻数的特点表示出其余两个数是解决本题的易错点.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 有两个如图所示的曲尺形框,框①和框②,用它们分别可以框住下表中的三个数(如图所
有两个如图所示的曲尺形框,框①和框②,用它们分别可以框住下表中的三个数(如图所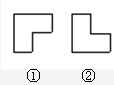 给示例),设被框住的三个数中最小的数为a.
给示例),设被框住的三个数中最小的数为a.