题目内容
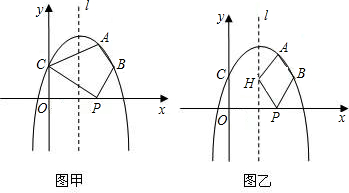
如图,已知抛物线y=ax2+bx+c过A(3,3.5)、B(4,2)、C(0,2)三点,点P是x轴上的动点.(1)求抛物线的解析式;
(2)如图甲所示,连接AC、CP、PB、BA,是否存在点P,使四边形ABPC为等腰梯形?若存在,求出点P的坐标;若不存在,说明理由;
(3)点H是题中抛物线对称轴l上的动点,如图乙所示,求四边形AHPB周长的最小值.
分析:(1)利用待定系数法,将点A,B,C的坐标代入解析式即可求得;
(2)根据等腰梯形的判定方法分别从PC∥AB与BP∥AC去分析,注意不要漏解;
(3)首先确定点P与点H的位置,再求解各线段的长即可.
(2)根据等腰梯形的判定方法分别从PC∥AB与BP∥AC去分析,注意不要漏解;
(3)首先确定点P与点H的位置,再求解各线段的长即可.
解答:解:∵抛物线y=ax2+bx+c过A(3,3.5)、B(4,2)、C(0,2)三点,
∴
解得:
,
∴此抛物线的解析式为:y=-
x2+2x+2;
(2)∵A(3,3.5)、B(4,2)、C(0,2),
∴AC=
,AB=
,
①若PC∥AB,则过点B作BE∥x轴,过点A作AE∥y轴,交点为E,
∴AE=1.5,BE=1,
当
=
时,AB∥PC,
∴
=
,
∴OP=
,
∴点P的坐标为:(
,0),
∴BP=
,
∴AP≠BC,
∴此点不符合要求,舍去;
②若BP∥AC,则过点A作AE∥y轴,过点C作CE∥x轴,相交于点E,过点B作BF∥y 轴,
轴,
当
=
时,BP∥AC,
∴
=
,
解得:PF=4,
∴点P与点O重合,
∴PC=2≠AB.
∴此点不符合要求,舍去;
(3)过A作对称轴的对称点A′,过B作x轴对称点B′,连接A′B′,分别交对称轴与x轴于H点、P点,则这两点即为所求.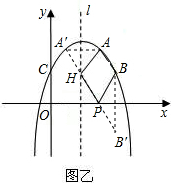
∴AH=A′H,PB=PB′,
∴AB+AH+PH+PB=AB+A′H+HP+PB′=AB+A′B′,
∵抛物线的y=-
x2+2x+2的对称轴为:x=2,
∵A(3,3.5),B(4,2),
∴A′(1,3.5),B′(4,-2),
∴AB=
,A′B′=
,
∴四边形AHPB周长的最小值为:
+
.
∴
|
解得:
|
∴此抛物线的解析式为:y=-
| 1 |
| 2 |
(2)∵A(3,3.5)、B(4,2)、C(0,2),
∴AC=
3
| ||
| 2 |
| ||
| 2 |

①若PC∥AB,则过点B作BE∥x轴,过点A作AE∥y轴,交点为E,
∴AE=1.5,BE=1,
当
| OC |
| AE |
| OP |
| BE |
∴
| 2 |
| 1.5 |
| OP |
| 1 |
∴OP=
| 4 |
| 3 |
∴点P的坐标为:(
| 4 |
| 3 |
∴BP=
| 10 |
| 3 |
∴AP≠BC,
∴此点不符合要求,舍去;
②若BP∥AC,则过点A作AE∥y轴,过点C作CE∥x轴,相交于点E,过点B作BF∥y
 轴,
轴,当
| AE |
| BF |
| CE |
| PF |
∴
| 1.5 |
| 3 |
| 2 |
| PF |
解得:PF=4,
∴点P与点O重合,
∴PC=2≠AB.
∴此点不符合要求,舍去;
(3)过A作对称轴的对称点A′,过B作x轴对称点B′,连接A′B′,分别交对称轴与x轴于H点、P点,则这两点即为所求.

∴AH=A′H,PB=PB′,
∴AB+AH+PH+PB=AB+A′H+HP+PB′=AB+A′B′,
∵抛物线的y=-
| 1 |
| 2 |
∵A(3,3.5),B(4,2),
∴A′(1,3.5),B′(4,-2),
∴AB=
| ||
| 2 |
| ||
| 2 |
∴四边形AHPB周长的最小值为:
| ||
| 2 |
| ||
| 2 |
点评:此题考查了待定系数法求二次函数的解析式,等腰梯形的判定与性质以及周长和最小问题.此题比较复杂,注意数形结合思想与分类讨论思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 C(0,3).
C(0,3). 、C(0,-3)两点,与x轴交于另一点B.
、C(0,-3)两点,与x轴交于另一点B. (2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1.
(2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1. 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B. 如图,已知抛物线y=ax2+bx+c的顶点是(-1,-4),且与x轴交于A、B(1,0)两点,交y轴于点C;
如图,已知抛物线y=ax2+bx+c的顶点是(-1,-4),且与x轴交于A、B(1,0)两点,交y轴于点C;