题目内容
【题目】如图,在△ABC中,AB=AC,∠A=36°,BD为角平分线,且AE=DE.
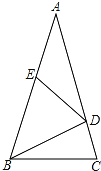
(1)写出图中三对相似比不为1的相似三角形 .
(2)选择(1)中一对加以证明.
【答案】(1)△ABC∽△BDC,△ABC∽△BDE,△EAD∽△DAB.(2)见解析
【解析】
试题分析:(1)利用等腰三角形的性质和三角形的内角和定理可计算出图中所有角的度数,然后根据有两组角对应相等的两个三角形相似可判断△ABC∽△BDC,△ABC∽△BDE,△EAD∽△DAB;
(2)利用等腰三角形的性质和三角形的内角和定理可计算出∠ABC=∠C=72°,再由BD为角平分线得到∠CBD=36°,于是根据有两组角对应相等的两个三角形相似可判断△ABC∽△BDC.
解:(1)△ABC∽△BDC,△ABC∽△BDE,△EAD∽△DAB.
故答案为△ABC∽△BDC,△ABC∽△BDE,△EAD∽△DAB.
(2)△ABC∽△BDC.理由如下:
∵AB=AC,∠A=36°,
∴∠ABC=∠C=![]() (180°﹣36°)=72°,
(180°﹣36°)=72°,
∵BD为角平分线,
∴∠CBD=36°,
∴∠A=∠CBD,∠BCD=∠ACB,
∴△ABC∽△BDC.

练习册系列答案
相关题目