题目内容
正方形ABCD和正方形DEFG如图①放置,保持正方形ABCD不动,将正方形DEFG绕点D顺时针旋转,旋转角为α(0°<α<180°)

(1)当0°<α<90°时,如图②,连结AE、CG,则AE:CG= ;
(2)当90°<α<180°时,如图③,连结AE、CG,(1)中的结论还成立吗?请说明理由;
(3)将图③中的正方形ABCD和正方形DEFG分别改为矩形ABCD和矩形DEFG,且使AD=4,CD=6,ED=2,GD=3,如图④,求AE:CG的值.

(1)当0°<α<90°时,如图②,连结AE、CG,则AE:CG= ;
(2)当90°<α<180°时,如图③,连结AE、CG,(1)中的结论还成立吗?请说明理由;
(3)将图③中的正方形ABCD和正方形DEFG分别改为矩形ABCD和矩形DEFG,且使AD=4,CD=6,ED=2,GD=3,如图④,求AE:CG的值.
(1)1;(2)成立,理由见试题解析;(3)2:3.
试题分析:(1)易证△ADE≌△CDG,即可得出AE:CG=1;
(2)与(1)类似,证明△ADE≌△CDG,即可得出AE:CG=1;
(3)证明△ADE∽△CDG即可.
试题解析:(1)∵正方形ABCD和正方形DEFG,∴AD=CD,DE=DG,∠ADC=∠EDG=90°,∴∠ADE=∠CDG,在△AED和△CGD中,∵AD=CD,∠ADE=∠CDG ,DE=DG,∴△ADE≌△CDG,∴AE=CG,∴AE:CG=1;
(2)成立,理由如下:
∵正方形ABCD和正方形DEFG,∴AD=CD,DE=DG,∠ADC=∠EDG=90°,∴∠ADE=∠CDG,在△AED和△CGD中,∵AD=CD,∠ADE=∠CDG ,DE=DG,∴△ADE≌△CDG,∴AE=CG,∴AE:CG=1;
(3)∵矩形ABCD和矩形DEFG,∴∠ADC=∠EDG=90°,∴∠ADE=∠CDG,∵
 ,
, ,∴
,∴ ,∴△ADE∽△CDG,∴AE:CG=AD:DC=4:6=2:3.
,∴△ADE∽△CDG,∴AE:CG=AD:DC=4:6=2:3.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


 (
( ,3)和
,3)和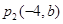 关于原点对称,则
关于原点对称,则 的值为( )
的值为( ) 

