题目内容
在下图中,直线l所对应的函数关系式为y=-| 1 | 5 |
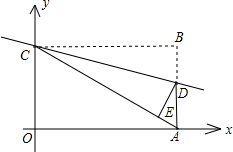 原点.
原点.(1)请直接写出线段OC的长;
(2)已知图中A点在x轴的正半轴上,四边形OABC为矩形,边AB与直线l相交于点D,沿直线l把△CBD折叠,点B恰好落在AC上一点E处,并且EA=1.
①试求点D的坐标;
②若⊙P的圆心在线段CD上,且⊙P既与直线AC相切,又与直线DE相交,设圆心P的横坐标为m,试求m的取值范围.
分析:(1)直线l所对应的函数关系式为y=-
x+5,则b=5,所以点C的坐标为(0,5),OC=5;
(2)①:设D点的横坐标为m,点D在直线l上,则它的纵坐标为:-
m+5由于四边形CBAO是矩形,有BC=OA=m,CA=CE+AE=m+1
在Rt△OAC中,由勾股定理知,OA2+OC2=AC2,即m2+52+(m+1)2,求解可得到m的值,从而求得D点的坐标为(12,
);
②由于△BCD和△CDE关于直线L对称,所以⊙P与直线AC相切,与DE相交相当于与直线BC相切,与BD相交,过点P作PM⊥OA,交OA于M,交BC于N,作PH⊥AB,交AB于H,由题意知:只要PN>PH即可,就可求得m的取值范围.
| 1 |
| 5 |
(2)①:设D点的横坐标为m,点D在直线l上,则它的纵坐标为:-
| 1 |
| 5 |
在Rt△OAC中,由勾股定理知,OA2+OC2=AC2,即m2+52+(m+1)2,求解可得到m的值,从而求得D点的坐标为(12,
| 13 |
| 5 |
②由于△BCD和△CDE关于直线L对称,所以⊙P与直线AC相切,与DE相交相当于与直线BC相切,与BD相交,过点P作PM⊥OA,交OA于M,交BC于N,作PH⊥AB,交AB于H,由题意知:只要PN>PH即可,就可求得m的取值范围.
解答:解:(1)OC=5;
(2)①解法一:设D点的横坐标为m,由已知得,
它的纵坐标为:-
m+5
∴BC=OA=m,CA=CE+AE=m+1,
在Rt△OAC中,OA2+OC2=AC2,即m2+52=(m+1)2,
解得m=12.
∴-
m+5=
,即D点的坐标为(12,
);
解法二:设D点的横坐标为m,由已知得,
它的纵坐标为:-
m+5,∴AD=-
m+5,DE=AB-AD=
m,
在Rt△ADE,EA2+ED2=AD2,即12+(
m)2=(-
m+5)2,解得m=12,
∴-
m+5=
,即D点的坐标为(12,
);
解法三:设D点的横坐标为m,由已知得,它的纵坐标为:-
m+5,
在Rt△OAC和Rt△ADE中,∠AOC=∠AED=90°,∠ACO+∠OAC=90°,∠OAC+∠EAD=90°,
∴∠ACO=∠EAD,
∴Rt△OAC∽Rt△ADE,
∴
=
,即:
=
,解得m=12,
∴-
m+5=
,即D点的坐标为(12,
);
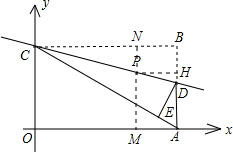
②由于△BCD和△CDE关于直线L对称,
所以⊙P与直线AC相切,与DE相交相当于与直线BC相切,与BD相交,
过点P作PM⊥OA,交OA于M,交BC于N;作PH⊥AB,交AB于H,
由题意知:只要PN>PH即可,
PN=MN-PM=
m,PH=12-m,即:
m>12-m,解得m>10,
又P在线段CD上,所以m≤12,
即m的取值范围是10<m≤12.
(2)①解法一:设D点的横坐标为m,由已知得,
它的纵坐标为:-
| 1 |
| 5 |
∴BC=OA=m,CA=CE+AE=m+1,
在Rt△OAC中,OA2+OC2=AC2,即m2+52=(m+1)2,
解得m=12.
∴-
| 1 |
| 5 |
| 13 |
| 5 |
| 13 |
| 5 |
解法二:设D点的横坐标为m,由已知得,
它的纵坐标为:-
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 5 |
在Rt△ADE,EA2+ED2=AD2,即12+(
| 1 |
| 5 |
| 1 |
| 5 |
∴-
| 1 |
| 5 |
| 13 |
| 5 |
| 13 |
| 5 |
解法三:设D点的横坐标为m,由已知得,它的纵坐标为:-
| 1 |
| 5 |
在Rt△OAC和Rt△ADE中,∠AOC=∠AED=90°,∠ACO+∠OAC=90°,∠OAC+∠EAD=90°,
∴∠ACO=∠EAD,
∴Rt△OAC∽Rt△ADE,
∴
| AC |
| AD |
| OC |
| AE |
| m+1 | ||
-
|
| 5 |
| 1 |
∴-
| 1 |
| 5 |
| 13 |
| 5 |
| 13 |
| 5 |

②由于△BCD和△CDE关于直线L对称,
所以⊙P与直线AC相切,与DE相交相当于与直线BC相切,与BD相交,
过点P作PM⊥OA,交OA于M,交BC于N;作PH⊥AB,交AB于H,
由题意知:只要PN>PH即可,
PN=MN-PM=
| 1 |
| 5 |
| 1 |
| 5 |
又P在线段CD上,所以m≤12,
即m的取值范围是10<m≤12.
点评:本题利用了:①折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;②一次函数的图象的性质,矩形的性质,相切的概念,全等三角形的判定和性质,勾股定理求解.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
探索、研究:下图是按照一定的规律画出的一列“树型”图,下表的n表示“树型”图的序号,an表示第n个“树型”图中“树枝”的个数.
图: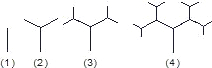
表:
(1)根据“图”、“表”可以归纳出an关于n的关系式为 .
若直线l1经过点(a1,a2)、(a2,a3),求直线l1对应的函数关系式,并说明对任意的正整数n,点(an,an+1)都在直线l1上.
(2)设直线l2:y=-x+4与x轴相交于点A,与直线l1相交于点M,双曲线y=
(x>0)经过点M,且与直线l2相交于另一点N.
①求点N的坐标,并在如图所示的直角坐标系中画出双曲线及直线l1、l2.
②设H为双曲线在点M、N之间的部分(不包括点M、N),P为H上一个动点,点P的横坐标为t,直线MP与x轴相交于点Q,当t为何值时,△MQA的面积等于△PMA的面积的2倍又是否存在t的值,使得△PMA的面积等于1?若存在,求出t的值;若不存在,请说明理由.
③在y轴上是否存在点G,使得△GMN的周长最小?若存在,求出点G的坐标;若不存在,请说明理由.
图:

表:
| n | 1 | 2 | 3 | 4 | … |
| an | 1 | 3 | 7 | 15 | … |
若直线l1经过点(a1,a2)、(a2,a3),求直线l1对应的函数关系式,并说明对任意的正整数n,点(an,an+1)都在直线l1上.
(2)设直线l2:y=-x+4与x轴相交于点A,与直线l1相交于点M,双曲线y=
| k |
| x |
①求点N的坐标,并在如图所示的直角坐标系中画出双曲线及直线l1、l2.
②设H为双曲线在点M、N之间的部分(不包括点M、N),P为H上一个动点,点P的横坐标为t,直线MP与x轴相交于点Q,当t为何值时,△MQA的面积等于△PMA的面积的2倍又是否存在t的值,使得△PMA的面积等于1?若存在,求出t的值;若不存在,请说明理由.
③在y轴上是否存在点G,使得△GMN的周长最小?若存在,求出点G的坐标;若不存在,请说明理由.

探索、研究:下图是按照一定的规律画出的一列“树型”图,下表的n表示“树型”图的序号,an表示第n个“树型”图中“树枝”的个数.
图: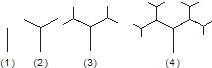
表:
| n | 1 | 2 | 3 | 4 | … |
| an | 1 | 3 | 7 | 15 | … |
若直线l1经过点(a1,a2)、(a2,a3),求直线l1对应的函数关系式,并说明对任意的正整数n,点(an,an+1)都在直线l1上.
(2)设直线l2:y=-x+4与x轴相交于点A,与直线l1相交于点M,双曲线y=
 (x>0)经过点M,且与直线l2相交于另一点N.
(x>0)经过点M,且与直线l2相交于另一点N.①求点N的坐标,并在如图所示的直角坐标系中画出双曲线及直线l1、l2.
②设H为双曲线在点M、N之间的部分(不包括点M、N),P为H上一个动点,点P的横坐标为t,直线MP与x轴相交于点Q,当t为何值时,△MQA的面积等于△PMA的面积的2倍又是否存在t的值,使得△PMA的面积等于1?若存在,求出t的值;若不存在,请说明理由.
③在y轴上是否存在点G,使得△GMN的周长最小?若存在,求出点G的坐标;若不存在,请说明理由.
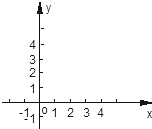
(2007•镇江)探索、研究:下图是按照一定的规律画出的一列“树型”图,下表的n表示“树型”图的序号,an表示第n个“树型”图中“树枝”的个数.
图: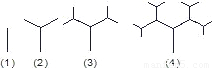
表:
(1)根据“图”、“表”可以归纳出an关于n的关系式为______.
若直线l1经过点(a1,a2)、(a2,a3),求直线l1对应的函数关系式,并说明对任意的正整数n,点(an,an+1)都在直线l1上.
(2)设直线l2:y=-x+4与x轴相交于点A,与直线l1相交于点M,双曲线y=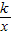 (x>0)经过点M,且与直线l2相交于另一点N.
(x>0)经过点M,且与直线l2相交于另一点N.
①求点N的坐标,并在如图所示的直角坐标系中画出双曲线及直线l1、l2.
②设H为双曲线在点M、N之间的部分(不包括点M、N),P为H上一个动点,点P的横坐标为t,直线MP与x轴相交于点Q,当t为何值时,△MQA的面积等于△PMA的面积的2倍又是否存在t的值,使得△PMA的面积等于1?若存在,求出t的值;若不存在,请说明理由.
③在y轴上是否存在点G,使得△GMN的周长最小?若存在,求出点G的坐标;若不存在,请说明理由.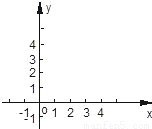
图:

表:
| n | 1 | 2 | 3 | 4 | … |
| an | 1 | 3 | 7 | 15 | … |
若直线l1经过点(a1,a2)、(a2,a3),求直线l1对应的函数关系式,并说明对任意的正整数n,点(an,an+1)都在直线l1上.
(2)设直线l2:y=-x+4与x轴相交于点A,与直线l1相交于点M,双曲线y=
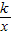 (x>0)经过点M,且与直线l2相交于另一点N.
(x>0)经过点M,且与直线l2相交于另一点N.①求点N的坐标,并在如图所示的直角坐标系中画出双曲线及直线l1、l2.
②设H为双曲线在点M、N之间的部分(不包括点M、N),P为H上一个动点,点P的横坐标为t,直线MP与x轴相交于点Q,当t为何值时,△MQA的面积等于△PMA的面积的2倍又是否存在t的值,使得△PMA的面积等于1?若存在,求出t的值;若不存在,请说明理由.
③在y轴上是否存在点G,使得△GMN的周长最小?若存在,求出点G的坐标;若不存在,请说明理由.

(2007•镇江)探索、研究:下图是按照一定的规律画出的一列“树型”图,下表的n表示“树型”图的序号,an表示第n个“树型”图中“树枝”的个数.
图: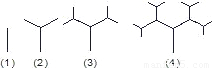
表:
(1)根据“图”、“表”可以归纳出an关于n的关系式为______.
若直线l1经过点(a1,a2)、(a2,a3),求直线l1对应的函数关系式,并说明对任意的正整数n,点(an,an+1)都在直线l1上.
(2)设直线l2:y=-x+4与x轴相交于点A,与直线l1相交于点M,双曲线y=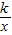 (x>0)经过点M,且与直线l2相交于另一点N.
(x>0)经过点M,且与直线l2相交于另一点N.
①求点N的坐标,并在如图所示的直角坐标系中画出双曲线及直线l1、l2.
②设H为双曲线在点M、N之间的部分(不包括点M、N),P为H上一个动点,点P的横坐标为t,直线MP与x轴相交于点Q,当t为何值时,△MQA的面积等于△PMA的面积的2倍又是否存在t的值,使得△PMA的面积等于1?若存在,求出t的值;若不存在,请说明理由.
③在y轴上是否存在点G,使得△GMN的周长最小?若存在,求出点G的坐标;若不存在,请说明理由.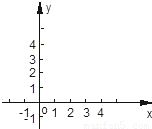
图:

表:
| n | 1 | 2 | 3 | 4 | … |
| an | 1 | 3 | 7 | 15 | … |
若直线l1经过点(a1,a2)、(a2,a3),求直线l1对应的函数关系式,并说明对任意的正整数n,点(an,an+1)都在直线l1上.
(2)设直线l2:y=-x+4与x轴相交于点A,与直线l1相交于点M,双曲线y=
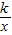 (x>0)经过点M,且与直线l2相交于另一点N.
(x>0)经过点M,且与直线l2相交于另一点N.①求点N的坐标,并在如图所示的直角坐标系中画出双曲线及直线l1、l2.
②设H为双曲线在点M、N之间的部分(不包括点M、N),P为H上一个动点,点P的横坐标为t,直线MP与x轴相交于点Q,当t为何值时,△MQA的面积等于△PMA的面积的2倍又是否存在t的值,使得△PMA的面积等于1?若存在,求出t的值;若不存在,请说明理由.
③在y轴上是否存在点G,使得△GMN的周长最小?若存在,求出点G的坐标;若不存在,请说明理由.



