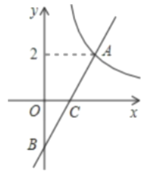
题目内容
【题目】如图,正方形ABCD的对角线AC,BD相交于点O,点E是AC的一点,连接EB,过点A做AM⊥BE,垂足为M,AM与BD相交于点F.
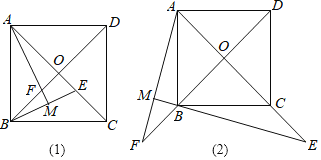
(1)猜想:如图(1)线段OE与线段OF的数量关系为 ;
(2)拓展:如图(2),若点E在AC的延长线上,AM⊥BE于点M,AM、DB的延长线相交于点F,其他条件不变,(1)的结论还成立吗?如果成立,请仅就图(2)给出证明;如果不成立,请说明理由.
【答案】(1)![]() ;(2)成立.理由见解析.
;(2)成立.理由见解析.
【解析】
(1)根据正方形的性质对角线垂直且平分,得到OB=OA,又因为AM⊥BE,所以∠MEA+∠MAE=90°=∠AFO+∠MAE,从而求证出Rt△BOE≌Rt△AOF,得到OE=OF.
(2)根据第一步得到的结果以及正方形的性质得到OB=OA,再根据已知条件求证出Rt△BOE≌Rt△AOF,得到OE=OF.
解:(1)正方形ABCD的对角线AC、BD相交于点O,AM⊥BE,
∴∠AOB=∠BOE=∠AMB=90°,
∵∠AFO=∠BFM(对顶角相等),
∴∠OAF=∠OBE(等角的余角相等),
又OA=OB(正方形的对角线互相垂直平分且相等),
∴△BOE≌△AOF(ASA),
∴OE=OF.
故答案为:OE=OF;
(2)成立.理由如下:
证明:∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]()
又∵![]() ,
,
∴![]() ,
,![]() ,
,
又∵![]()
∴![]() ∴
∴![]() ,
,
∴![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目