题目内容
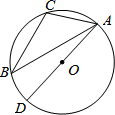如图，⊙O是△ABC的外接圆，AD是⊙O的直径，若⊙O的半径为3，sinB=| 1 |
| 3 |
考点：圆周角定理,锐角三角函数的定义
专题：计算题
分析：先求出圆的直径，连接CD，由圆周角定理可知，∠B=∠D，∠ACD=90°，再由sinB=
，可知sinD=
=
，故可得出结论．
| 1 |
| 3 |
| AC |
| AD |
| 1 |
| 3 |
解答：
解：∵AD是⊙O的直径，⊙O的半径为3，
∴AD=2OA=2×3=6，
连接CD，
∵∠B、∠D是
所对的圆周角，AD是⊙O的直径，
∴∠B=∠D，∠ACD=90°，
∵sinB=
，
∴sinD=
=
，即
=
，解得AC=2．
故答案为：2．
解：∵AD是⊙O的直径，⊙O的半径为3，∴AD=2OA=2×3=6，
连接CD，
∵∠B、∠D是
 |
| AC |
∴∠B=∠D，∠ACD=90°，
∵sinB=
| 1 |
| 3 |
∴sinD=
| AC |
| AD |
| 1 |
| 3 |
| AC |
| 6 |
| 1 |
| 3 |
故答案为：2．
点评：本题考查的是圆周角定理，根据题意作出辅助线，构造出圆周角是解答此题的关键．
练习册系列答案
黎明文化寒假作业系列答案
相关题目