题目内容
【题目】如图,平行四边形ABCD中,∠B=60°.G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连结CE,DF,下列说法不正确的是( )
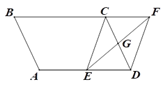
A. 四边形CEDF是平行四边形
B. 当![]() 时,四边形CEDF是矩形
时,四边形CEDF是矩形
C. 当![]() 时,四边形CEDF是菱形
时,四边形CEDF是菱形
D. 当![]() 时,四边形CEDF是菱形
时,四边形CEDF是菱形
【答案】C
【解析】分析:根据已知条件易证△CFG≌△EDG,可得FG=EG,CG=DG,根据对角线互相平分的四边形为平行四边形即可判定四边形CEDF是平行四边形;再由CE⊥AD,根据有一个角为直角的平行四边形为矩形即可判定平行四边形CEDF是矩形;再证明△CED为等边三角形,可得CE=DE,根据一组邻边相等的平行四边形为菱形即可得平行四边形CEDF是菱形;采用排除法即可得答案.
详解:
∵四边形ABCD是平行四边形,
∴CF∥ED,
∴∠FCD=∠GCD,
∵G是CD的中点,
∴CG=DG,
在△FCG和△EDG中,
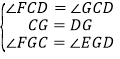 ,
,
∴△CFG≌△EDG(ASA),
∴FG=EG,
∵CG=DG,
∴四边形CEDF是平行四边形;
∵CE⊥AD,
∴平行四边形CEDF是矩形;
∵四边形ABCD是平行四边形,
∴∠B=∠ADC=60°;
∵∠AEC=120°,
∴∠DEC=60°;
∴∠DEC=∠ADC=60°,
∴△CED为等边三角形,
∴CE=DE,
∴平行四边形CEDF是菱形;
综上,选项A、B、D正确,选项D错误,故选C.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案【题目】按要求画图,并解答问题
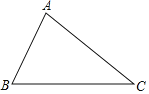
(1)如图,取BC边的中点D,画射线AD;
(2)分别过点B、C画BE⊥AD于点E,CF⊥AD于点F;
(3)BE和CF的位置关系是 ;通过度量猜想BE和CF的数量关系是 .
【题目】某学校准备为七年级学生开设![]() 共6门选修课,选取了若干学生进行了我最喜欢的一门选修课调查,将调查结果绘制成了如图所示的统计图表(不完整).
共6门选修课,选取了若干学生进行了我最喜欢的一门选修课调查,将调查结果绘制成了如图所示的统计图表(不完整).
选修课 |
|
|
|
|
|
|
人数 | 40 | 60 | 100 |
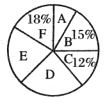
下列说法不正确的是( )
A.这次被调查的学生人数为400人B.![]() 对应扇形的圆心角为
对应扇形的圆心角为![]()
C.喜欢选修课![]() 的人数为72人D.喜欢选修课
的人数为72人D.喜欢选修课![]() 的人数最少
的人数最少