题目内容
 如图,点E、F分别在正方形ABCD的边CD、AD上,且AB=2CE=3AF,过F作FG⊥BE于P交BC于G,连接DP交BC于H,连BF、EF. 下列结论:
如图,点E、F分别在正方形ABCD的边CD、AD上,且AB=2CE=3AF,过F作FG⊥BE于P交BC于G,连接DP交BC于H,连BF、EF. 下列结论:①△PBF为等腰直角三角形;②H为BC的中点;③∠DEF=2∠PFE;④
| S△PHG |
| S△PDE |
| 2 |
| 3 |
其中正确的结论( )
分析:如图,①绕点B将△EBC逆时针旋转90°得△ABM,就有AM=CE,由勾股定理可以求出EF的值,通过证明△EFB≌△MFB就可以求出①;根据△BPG∽△BCE就可以求出PG、BG从而求出GC,再求△HPG∽△DPF得出GH的值就可以得出HC的值,从而得出②的结论;由△BCE≌△DCH可以得出∠1=∠4,根据四点共圆的性质可以得出∠4=∠5,进而由角的关系得出∠9=∠5而得出③成立;根据△BHP≌△DEP就可以得出面积相等,根据等高的两三角形的面积关系等于底之比就可以求出结论.
解答:解:如图,①绕点B将△EBC逆时针旋转90°得△ABM,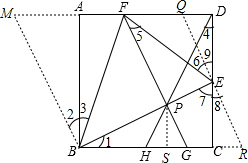
∴AM=CE,BE=BM,∠1=∠2.∠BAM=∠BCE.
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠ABC=∠BCD=∠CDA=∠DAB=90°.AD∥BC.
∴∠BAM=∠BCE=90°,
∴∠MAF=180°,
∴点M、A、F在同一直线上.
∵AB=2CE=3AF,设AF=x,
∴AB=3x,CE=1.5x,
∴MF=1.5x+x=2.5x,FD=3x-x=2x,ED=1.5x.
在Rt△DFE中,由勾股定理得EF=2.5x,
∴EF=MF.
∵在△EFB和△MFB中,
,
∴△EFB≌△MFB(SSS),
∴∠EBF=∠MBF.
∵∠MBF=∠2+∠3,
∴∠MBF=∠1+∠3,
∴∠EBF=∠1+∠3.
∵∠EBF+∠1+∠3=90°,
∴∠EBF=45°.
∵FG⊥BE,
∴∠FPB=∠BPG=90°,
∴∠BFP=45°,
∴∠BFP=∠PBF,
∴PF=PB,
∴△PBF为等腰直角三角形,故①正确;
在Rt△AFB中,由勾股定理得BF=
x,
在Rt△BFP中,由勾股定理得PF=PB=
x,
在Rt△BEC中,由勾股定理得BE=
x,
∵∠1=∠1,∠BPG=∠BCE=90°,
∴△BPG∽△BCE,
∴
=
=
,
∴
=
=
,
∴PG=
x,BG=2.5x.
∴GC=0.5x.
∵AD∥BC,
∴△HPG∽△DPF,
∴
=
,
∴
=
,
∴GH=x,
∴HC=1.5x,
∴2HC=3x,
∴2HC=BC,
∴H是BC的中点.故②正确;
∵AB=2CE,
∴2HC=2CE,
∴HC=CE,
在△BCE和△DCH中,
,
∴△BCE≌△DCH(SAS),
∴∠1=∠4.
过点E作QR∥FG交AD于Q,交BC的延长线于R.
∴∠BER=∠APG=90°,∠5=∠6.
∴∠7+∠8=90°.
∵∠1+∠7=90°,
∴∠1=∠8.
∵∠8=∠9,
∴∠1=∠9,
∴∠4=∠9.
∵∠FPE=∠FDE=90°,
∴F、P、E、D四点共圆,
∴∠4=∠5.
∴∠9=∠5,
∴∠DEF=2∠5,
即∠DEF═2∠PFE.故③正确;
∵在△BHP和△DEP中,
,
∴△BHP≌△DEP(AAS),
∴S△BHP=S△DEP.
作PS⊥BC于S,
∴S△BHP=
,S△PHG=
.
∴S△BHP=
,S△PHG=
,
∴
=
=
=
,故④正确.
∴①②③④都是正确的.
故选D.

∴AM=CE,BE=BM,∠1=∠2.∠BAM=∠BCE.
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠ABC=∠BCD=∠CDA=∠DAB=90°.AD∥BC.
∴∠BAM=∠BCE=90°,
∴∠MAF=180°,
∴点M、A、F在同一直线上.
∵AB=2CE=3AF,设AF=x,
∴AB=3x,CE=1.5x,
∴MF=1.5x+x=2.5x,FD=3x-x=2x,ED=1.5x.
在Rt△DFE中,由勾股定理得EF=2.5x,
∴EF=MF.
∵在△EFB和△MFB中,
|
∴△EFB≌△MFB(SSS),
∴∠EBF=∠MBF.
∵∠MBF=∠2+∠3,
∴∠MBF=∠1+∠3,
∴∠EBF=∠1+∠3.
∵∠EBF+∠1+∠3=90°,
∴∠EBF=45°.
∵FG⊥BE,
∴∠FPB=∠BPG=90°,
∴∠BFP=45°,
∴∠BFP=∠PBF,
∴PF=PB,
∴△PBF为等腰直角三角形,故①正确;
在Rt△AFB中,由勾股定理得BF=
| 10 |
在Rt△BFP中,由勾股定理得PF=PB=
| 5 |
在Rt△BEC中,由勾股定理得BE=
| 3 |
| 2 |
| 5 |
∵∠1=∠1,∠BPG=∠BCE=90°,
∴△BPG∽△BCE,
∴
| PG |
| CE |
| PB |
| BC |
| BG |
| BE |
∴
| PG |
| 1.5x |
| ||
| 3x |
| BG | ||||
|
∴PG=
| ||
| 2 |
∴GC=0.5x.
∵AD∥BC,
∴△HPG∽△DPF,
∴
| GH |
| DF |
| PG |
| PF |
∴
| GH |
| 2x |
| ||||
|
∴GH=x,
∴HC=1.5x,
∴2HC=3x,
∴2HC=BC,
∴H是BC的中点.故②正确;
∵AB=2CE,
∴2HC=2CE,
∴HC=CE,
在△BCE和△DCH中,
|
∴△BCE≌△DCH(SAS),
∴∠1=∠4.
过点E作QR∥FG交AD于Q,交BC的延长线于R.
∴∠BER=∠APG=90°,∠5=∠6.
∴∠7+∠8=90°.
∵∠1+∠7=90°,
∴∠1=∠8.
∵∠8=∠9,
∴∠1=∠9,
∴∠4=∠9.
∵∠FPE=∠FDE=90°,
∴F、P、E、D四点共圆,
∴∠4=∠5.
∴∠9=∠5,
∴∠DEF=2∠5,
即∠DEF═2∠PFE.故③正确;
∵在△BHP和△DEP中,
|
∴△BHP≌△DEP(AAS),
∴S△BHP=S△DEP.
作PS⊥BC于S,
∴S△BHP=
| BH•PS |
| 2 |
| HG•PS |
| 2 |
∴S△BHP=
| 1.5x•PS |
| 2 |
| x•PS |
| 2 |
∴
| S△PHG |
| S△PDE |
| S△PHG |
| S△PHB |
| ||
|
| 2 |
| 3 |
∴①②③④都是正确的.
故选D.
点评:本题考查了正方形的性质的运用,旋转的性质的运用,全等三角形的判定及性质的运用,勾股定理的运用,四点共圆定理的运用,相似三角形的判定及性质的运用.解答时作出需要的辅助线是关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
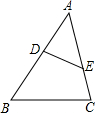 如图,点D、E分别在△ABC的边上AB、AC上,且∠AED=∠ABC,若DE=3,BC=6,AB=8,则AE的长为
如图,点D、E分别在△ABC的边上AB、AC上,且∠AED=∠ABC,若DE=3,BC=6,AB=8,则AE的长为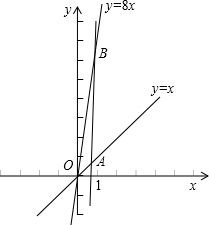 如图,点A,B分别在一次函数y=x,y=8x的图象上,其横坐标分别为a,b (a>0,b>0 ).若直线AB为一次函数y=kx+m的图象,则当
如图,点A,B分别在一次函数y=x,y=8x的图象上,其横坐标分别为a,b (a>0,b>0 ).若直线AB为一次函数y=kx+m的图象,则当 19、如图,点M、N分别在正三角形ABC的BC、CA边上,且BM=CN,AM、BN交于点Q,求∠AQN的度数.
19、如图,点M、N分别在正三角形ABC的BC、CA边上,且BM=CN,AM、BN交于点Q,求∠AQN的度数. 12、如图,点D、E分别在∠BAC的边上,连接DC、BE,若∠B=∠C,那么补充下列一个条件后,仍无法判定△ABE≌△ACD的是( )
12、如图,点D、E分别在∠BAC的边上,连接DC、BE,若∠B=∠C,那么补充下列一个条件后,仍无法判定△ABE≌△ACD的是( ) 如图,点A、B分别在直线l1、l2上,过点A作到l2的距离AM,过点B作直线l3∥l1.
如图,点A、B分别在直线l1、l2上,过点A作到l2的距离AM,过点B作直线l3∥l1.