题目内容
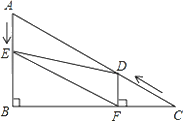
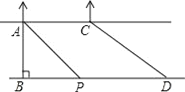
【题目】某数学兴趣小组想测量河流的宽度AB,河流两岸AC,BD互相平行,河流对岸有两棵树A和C,且A.C之间的距离是60m,他们在D处测得∠BDC=36°,前行140米后测得∠BPA=45°,请根据这些数据求出河流的宽度.(结果精确到0.1米,参考数据:tan36°≈0.73,sin36°≈0.59,cos36°≈0.81)
【答案】河流的宽度约为216.3米
【解析】
作CH⊥BD,则BH=AC=60米,设AB为x米,则CH为x米,在Rt△ABP中,由∠BPA=45°,可得BP=x,然后表示出HD的长,在Rt△CHD中,利用∠CDH的正切列方程求解即可.
作CH⊥BD,则BH=AC=60米,设AB为x米,则CH为x米,

在Rt△ABP中,tan45°=1,
∴BP=x,
∴HD=BP+PD-BH=x+140-60=(x+80)米,
在Rt△CHD中,
∵tan∠CDH= ![]() =
=![]() ,
,
∴x=(x+80)tan36°,
∴x≈216.3(米),
答:河流的宽度约为216.3米

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目