题目内容
【题目】【问题情境】
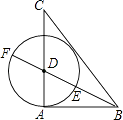
在△ABC中,AB=AC,点P为BC所在直线上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D、E,过点C作CF⊥AB,垂足为F.当P在BC边上时(如图1),求证:PD+PE=CF.

图① 图② 图③
证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.(不要证明)
【变式探究】
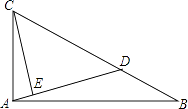
当点P在CB延长线上时,其余条件不变(如图3).试探索PD、PE、CF之间的数量关系并说明理由.
请运用上述解答中所积累的经验和方法完成下列两题:
【结论运用】
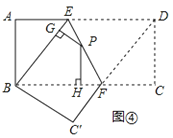
如图4,将长方形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE、PH⊥BC,垂足分别为G、H,若AD=8,CF=3,求PG+PH的值;
【迁移拓展】
在直角坐标系中.直线l1:y=![]() 与直线l2:y=2x+4相交于点A,直线l1、l2与x轴分别交于点B、点C.点P是直线l2上一个动点,若点P到直线l1的距离为1.求点P的坐标.
与直线l2:y=2x+4相交于点A,直线l1、l2与x轴分别交于点B、点C.点P是直线l2上一个动点,若点P到直线l1的距离为1.求点P的坐标.

【答案】【变式探究】:详见解析;【结论运用】:4;【迁移拓展】:P1的坐标为(![]() ,3)或(
,3)或(![]() ,5)
,5)
【解析】试题分析:【变式探究】按照【问题情境】的证明思路即可解决问题.
【结论运用】过![]() 作
作![]() 利用问题情境中的结论可得
利用问题情境中的结论可得![]() ,易证
,易证![]() 只需求即可.
只需求即可.
【迁移拓展】分成两种情况进行讨论.
试题解析:【变式探究】:连接![]()
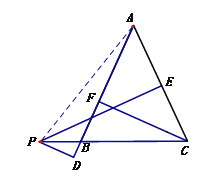
∵PD⊥AB,PE⊥AC,CF⊥AB,
![]()
![]()
![]()
![]()
【结论运用】过![]() 作
作![]() 垂足为
垂足为![]() ,如图④,
,如图④,
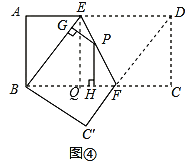
∵四边形![]() 是长方形,
是长方形, ![]()
![]()
由折叠可得: ![]()
![]()
![]()
![]()
![]()
∴四边形![]() 是长方形.
是长方形. ![]()
∵AD∥BC, ![]()
![]()
由问题情境中的结论可得: ![]()
![]() 的值为4.
的值为4.
【迁移拓展】
由题意得: ![]()
![]()
![]()
![]()
(1)由结论得: ![]()

![]()
即点![]() 的纵坐标为3,
的纵坐标为3,
又点![]() 在直线l2上 ∴
在直线l2上 ∴![]() =3 ,
=3 ,
∴![]() .
.
即点![]() 的坐标为
的坐标为![]()
(2) 由结论得: ![]()
![]() 即点
即点![]() 的纵坐标为5,
的纵坐标为5,
又点![]() 在直线l2上 ∴
在直线l2上 ∴![]() =5.
=5.
∴![]() .
.
即点![]() 的坐标为
的坐标为![]()

 轻松暑假总复习系列答案
轻松暑假总复习系列答案