题目内容
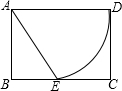
如图,已知矩形纸片ABCD,AD=2,AB= ,以A为圆心,AD长为半径画弧交BC于点E,将扇形AED剪下围成一个圆锥,则该圆锥的底面半径为 .
,以A为圆心,AD长为半径画弧交BC于点E,将扇形AED剪下围成一个圆锥,则该圆锥的底面半径为 .

【答案】

【解析】
试题分析:依题意知,以A为圆心,AD长为半径画弧交BC于点E,∴AD=AE=2.cos∠EAB= =
= 。∴∠EAB=30°。又∵纸片为矩形ABCD,∴∠BAD=90°,∴∠DAE=60°。所以扇形AED弧长l= n(圆心角)× π(圆周率)×r(半径)/180=60°× 2/180°=
。∴∠EAB=30°。又∵纸片为矩形ABCD,∴∠BAD=90°,∴∠DAE=60°。所以扇形AED弧长l= n(圆心角)× π(圆周率)×r(半径)/180=60°× 2/180°=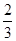 π。此扇形围成圆锥,则圆锥的底面周长C等于扇形弧长。所以圆锥的底面半径r=
π。此扇形围成圆锥,则圆锥的底面周长C等于扇形弧长。所以圆锥的底面半径r=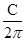 =
=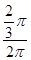 =
= 。
。
考点:考查扇形弧长公式,直角三角形特殊角三角函数值及计算,考查圆锥底面周长与扇形弧长的关系及周长与半径的转化公式。
点评:难度较低,主要考查扇形弧长公式,直角三角形特殊角三角函数值及计算,考查圆锥底面周长与扇形弧长的关系及周长与半径的转化公式。能够运用各公式直接进行转换计算即可。

练习册系列答案
相关题目

 如图,已知矩形纸片ABCD,AD=2,AB=
如图,已知矩形纸片ABCD,AD=2,AB=
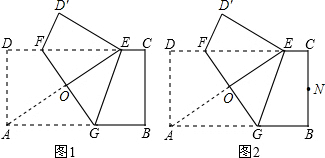 A与边CD上的点E重合,折痕FG分别与AB,CD交于点G,F,AE与FG交于点O.
A与边CD上的点E重合,折痕FG分别与AB,CD交于点G,F,AE与FG交于点O.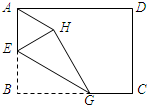 (2012•安庆二模)如图,已知矩形纸片ABCD,E是AB边的中点,点G为BC边上的一点,现沿EG将纸片折叠,使点B落在纸片上的点H处,连接AH.若AB=EG,则与∠BEG相等的角的个数为( )
(2012•安庆二模)如图,已知矩形纸片ABCD,E是AB边的中点,点G为BC边上的一点,现沿EG将纸片折叠,使点B落在纸片上的点H处,连接AH.若AB=EG,则与∠BEG相等的角的个数为( )