Question

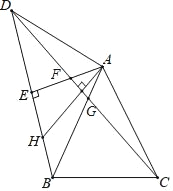
【题目】如图，△ABC和△ECD都是等边三角形，B、C、D三点在一条直线上，AD与BE相交于点O，AD与CE相交于点F，AC与BE相交于点G．

（1）△BCE与△ACD全等吗？请说明理由．

（2）求∠BOD度数．

Answer 1

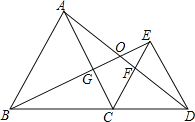
【答案】（1）△BCE≌△ACD．证明见解析;(2)120°.

【解析】

（1）通过观察图形，根据等边三角形的性质就可以证明△BCE≌△ACD；

（2）由（1）△BCE≌△ACD可以得出∠ADC=∠BEC，而有∠AOB=∠EBC+∠ADB，就有∠AOB=∠EBC+∠BEC=∠DCE=60°，从而可以求出∠BOD的值．

（1）△BCE≌△ACD．

理由：∵△ABC和△ECD都是等边三角形，

∴BC=AC，CE=CD，∠BCA=∠ECD=∠BAC=60°，

∴∠BCA+∠ACE=∠ECD+∠ACE，

∵∠BCE=∠ACD．

在△BCE和△ACD中，

，

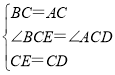∴△BCE≌△ACD（SAS）；

（2）∵△BCE≌△ACD，

∴∠ADC=∠BEC．

∵∠AOB=∠EBC+∠ADC，

∴∠AOB=∠EBC+∠BEC=∠DCE=60°．

∵∠AOB+∠BOD=180°，

∴∠BOD=120°．