��Ŀ����
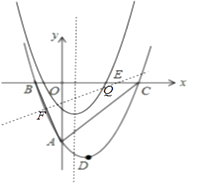
����Ŀ����ͼ��������A��0��6����������y= ![]() x2+bx+c��x���ཻ��B����2��0����C���㣮
x2+bx+c��x���ཻ��B����2��0����C���㣮
��1����������ߵĺ�����ϵʽ�Ͷ���D�����ꣻ
��2����ֱ��AC����Ӧ�ĺ�����ϵʽ��
��3������1������õ�����������ƽ��1����λ���ȣ�������ƽ��m��m��0������λ���ȵõ���������y1 �� ����������y1�Ķ���P�ڡ�ABC�ڣ���m��ȡֵ��Χ��
��4���ڣ�3���Ľ����£���������y1���Ƿ���ڵ�Q��ʹ�á�QAB����ABΪ�ױߵĵ��������Σ���������п��ܳ��ֵ��������ֱ��д�����Ӧ��m��ȡֵ��Χ��
���𰸡�
��1��
�⣺��A��0����6����B����2��0������y= ![]() x2+bx+c��
x2+bx+c�� ![]() �����
����� ![]() ��
��
���������߽���ʽΪy= ![]() x2��2x��6��
x2��2x��6��
��Ϊy= ![]() ��x��2��2��8��
��x��2��2��8��
���Զ���D������Ϊ��2����8����
��2��
�⣺��y=0ʱ�� ![]() x2��2x��6=0�����x1=��2��x2=6����C��6��0����
x2��2x��6=0�����x1=��2��x2=6����C��6��0����
��ֱ��AC�Ľ���ʽΪy=mx+n��
��A��0����6����C��6��0������� ![]() �����
����� ![]() ��
��
����ֱ��AC�Ľ���ʽΪy=x��6��
��3��
�⣺������y= ![]() ��x��2��2��8����ƽ��1����λ���ȣ�������ƽ��m��m��0������λ���ȵõ���������y1�Ľ���ʽΪy=
��x��2��2��8����ƽ��1����λ���ȣ�������ƽ��m��m��0������λ���ȵõ���������y1�Ľ���ʽΪy= ![]() ��x��1��2��8+m��
��x��1��2��8+m��
��x=1ʱ��y=x��6=��5��
����������y1�Ķ���P�ڡ�ABC�ڣ�
�ੁ5����8+m��0��
��3��m��8��
��4��
�⣺��AB�Ĵ�ֱƽ���߽�x����E����AB��F����ͼ��
AB= ![]() =2
=2 ![]() ����BF=
����BF= ![]() ��
��
�ߡ�BEF=��BAO��
��Rt��BEF��Rt��BAO��
�� ![]() =
= ![]() ����
���� ![]() =
= ![]() �����BE=10��
�����BE=10��
��E��8��0����
��F����1����3����
��ֱ��EF�Ľ���ʽΪy=kx+b��
��E��8��0����F����1����3������� ![]() �����
����� 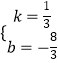 ��
��
��ֱ��EF�Ľ���ʽΪy= ![]() x��
x�� ![]() ��
��
�ѷ��� ![]() ��x��1��2��8+m=
��x��1��2��8+m= ![]() x��
x�� ![]() ��������3x2��8x+6m��29=0��
��������3x2��8x+6m��29=0��
��=����8��2��4��3����6m��29��=��72m+412��
����=0������72m+412=0�����m= ![]() ʱ��������y1��ֱ��EFֻ��һ�������㣬��ʱ������y1�ϴ���һ����Q��ʹ�á�QAB����ABΪ�ױߵĵ��������Σ�
ʱ��������y1��ֱ��EFֻ��һ�������㣬��ʱ������y1�ϴ���һ����Q��ʹ�á�QAB����ABΪ�ױߵĵ��������Σ�
������0������72m+412��0�����m�� ![]() ����m�ķ�ΧΪ3��m��
����m�ķ�ΧΪ3��m�� ![]() ��������y1��ֱ��EF�����������㣬��ʱ������y1�ϴ���������Q��ʹ�á�QAB����ABΪ�ױߵĵ��������Σ�
��������y1��ֱ��EF�����������㣬��ʱ������y1�ϴ���������Q��ʹ�á�QAB����ABΪ�ױߵĵ��������Σ�
������0������72m+412��0�����m�� ![]() ʱ����m�ķ�ΧΪ
ʱ����m�ķ�ΧΪ ![]() ��m��8������������y1��ֱ��EFû�й����㣬��ʱ������y1�ϲ�����һ����Q��ʹ�á�QAB����ABΪ�ױߵĵ��������Σ�
��m��8������������y1��ֱ��EFû�й����㣬��ʱ������y1�ϲ�����һ����Q��ʹ�á�QAB����ABΪ�ױߵĵ��������Σ�
����������1����A���B���������y= ![]() x2+bx+c�ù���b��c�ķ����飬Ȼ��ⷽ�����b��c���ɵõ������߽���ʽ��Ȼ���һ��ʽ��ɶ���ʽ�ɵö���D�����ꣻ��2���Ƚⷽ��
x2+bx+c�ù���b��c�ķ����飬Ȼ��ⷽ�����b��c���ɵõ������߽���ʽ��Ȼ���һ��ʽ��ɶ���ʽ�ɵö���D�����ꣻ��2���Ƚⷽ�� ![]() x2��2x��6=0��C��6��0����Ȼ�����ô���ϵ������ֱ��AC�Ľ���ʽ����3�����������ߵ�ƽ�ƹ��ɵõ���������y1�Ľ���ʽΪy=
x2��2x��6=0��C��6��0����Ȼ�����ô���ϵ������ֱ��AC�Ľ���ʽ����3�����������ߵ�ƽ�ƹ��ɵõ���������y1�Ľ���ʽΪy= ![]() ��x��1��2��8+m���ټ�����������ߵĶԳ�����ֱ��AC�Ľ������꣬�Ӷ��õ���5����8+m��0��Ȼ��ⲻ��ʽ�õ�m�ķ�Χ����4����AB�Ĵ�ֱƽ���߽�x����E����AB��F����ͼ��֤��Rt��BEF��Rt��BAO���������Ʊȼ����BE=10����E��8��0���������ô���ϵ������ȷ��ֱ��EF�Ľ���ʽΪy=
��x��1��2��8+m���ټ�����������ߵĶԳ�����ֱ��AC�Ľ������꣬�Ӷ��õ���5����8+m��0��Ȼ��ⲻ��ʽ�õ�m�ķ�Χ����4����AB�Ĵ�ֱƽ���߽�x����E����AB��F����ͼ��֤��Rt��BEF��Rt��BAO���������Ʊȼ����BE=10����E��8��0���������ô���ϵ������ȷ��ֱ��EF�Ľ���ʽΪy= ![]() x��
x�� ![]() ��Ȼ��ͨ���жϷ���
��Ȼ��ͨ���жϷ��� ![]() ��x��1��2��8+m=
��x��1��2��8+m= ![]() x��
x�� ![]() �ĸ������ȷ��������y1��ֱ��EF�Ĺ�����ĸ������Ӷ����ж���������y1���Ƿ���ڵ�Q��ʹ�á�QAB����ABΪ�ױߵĵ��������Σ���д����Ӧ��m�ķ�Χ��
�ĸ������ȷ��������y1��ֱ��EF�Ĺ�����ĸ������Ӷ����ж���������y1���Ƿ���ڵ�Q��ʹ�á�QAB����ABΪ�ױߵĵ��������Σ���д����Ӧ��m�ķ�Χ��
�����㾫�������ö��κ��������ʶ���Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��

 ѧ�����νӽ̲��Ͼ���ѧ������ϵ�д�
ѧ�����νӽ̲��Ͼ���ѧ������ϵ�д�����Ŀ���ֻ���2018�깲���ε�ij�̳����ձ�۹�����A��B������Ʒ���乺��������±���
����A��Ʒ������������ | ����B��Ʒ������������ | ����������Ʒ���ܷ��ã�Ԫ�� | |
��һ�ι��� | 6 | 5 | 1140 |
�ڶ��ι��� | 3 | 7 | 1110 |
��1���ֱ����A��B������Ʒ�ı�ۡ�
��2������̳�ʵ����ӭ2019�´����Ĵ������A��B������Ʒ���������ۿ�����ͬ�������ֻ�ǰ���̳���1062Ԫ�ֹ�����9��A��Ʒ��8��B��Ʒ�����ʱ��δ������A��B��Ʒ���ۿ�����Ϊ���٣��ڱ��ι����У��ֻ�����Լ�˶���Ǯ��
����Ŀ�������龰��
��ͼ����ֱ������ϵxOy�У���A��BΪ���κ���y=ax2��a��0��ͼ���ϵ����㣬�ҵ�A��B�ĺ�����ֱ�Ϊm��n��m��n��0��������OA��AB��OB�����AOB�����ΪSʱ������������⣺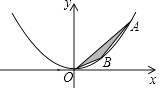
��1��̽������a=1ʱ��
mn | m��n | S | |
m=3��n=1 | 3 | 2 | |
m=5��n=2 | 10 | 3 |
��a=2ʱ��
2mn | m��n | S | |
m=3��n=1 | 6 | 2 | |
m=5��n=2 | 20 | 3 |
��2������֤����������m��n��m��n��0��������S=����a��m��n��ʾ������֤����IJ��룮
��3����չӦ�ã�
����A��B�ĺ�����ֱ�Ϊm��n��m��0��n����������������ʱ����AOB�����S=����a��m��n��ʾ����