题目内容
【题目】已知,点P是直角三角形ABC斜边AB上一动点(不与A,B重合),分别过点A,B向直线CP作垂线,垂足分别为E,F,Q为斜边AB的中点.
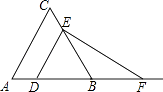
(1)当点P与点Q重合时,如图1,写出QE与QF的数量关系,不证明;
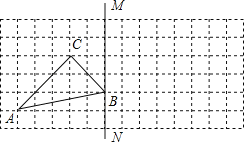
(2)当点P在线段AB上且不与点Q重合时,如图2,(1)的结论是否成立?并证明;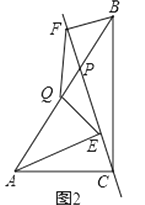
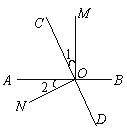
(3)当点P在线段BA(或AB)的延长线上时,如图3,此时(1)的结论是否成立?请画出图形并给予证明.
【答案】
(1)
解:QE=QF,
理由是:如图1,∵Q为AB中点,
∴AQ=BQ,
∵BF⊥CP,AE⊥CP,
∴∠BFQ=∠AEQ=90°,
在△BFQ和△AEQ中 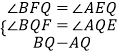
∴△BFQ≌△AEQ(AAS),
∴QE=QF,
(2)
解:中的结论仍然成立,
证明:如图2,延长FQ交AE于D,
∵Q为AB中点,
∴AQ=BQ,
∵BF⊥CP,AE⊥CP,
∴BF∥AE,
∴∠QAD=∠FBQ,
在△FBQ和△DAQ中, 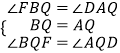 ,
,
∴△FBQ≌△DAQ(ASA),
∴QF=QD,
∵AE⊥CP,
∴EQ是Rt△DEF斜边上的中线,
∴QE=QF=QD,
即QE=QF.
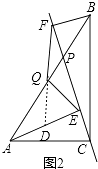
(3)
解:(1)中的结论仍然成立,
证明:如图3,
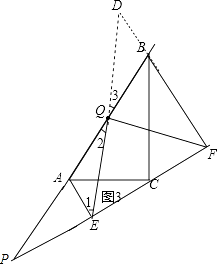
延长EQ、FB交于D,
∵Q为AB中点,
∴AQ=BQ,
∵BF⊥CP,AE⊥CP,
∴BF∥AE,
∴∠1=∠D,
在△AQE和△BQD中, 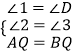 ,
,
∴△AQE≌△BQD(AAS),
∴QE=QD,
∵BF⊥CP,
∴FQ是Rt△DEF斜边DE上的中线,
∴QE=QF.
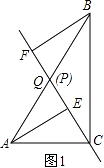
【解析】(1)证△BFQ≌△AEQ即可;(2)证△FBQ≌△DAQ,推出QF=QD,根据直角三角形斜边上中线性质求出即可;(3)证△AEQ≌△BDQ,推出DQ=QE,根据直角三角形斜边上中线性质求出即可
【考点精析】利用三角形的“三线”对题目进行判断即可得到答案,需要熟知1、三角形角平分线的三条角平分线交于一点(交点在三角形内部,是三角形内切圆的圆心,称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部,是三角形的几何中心,称为中心);3、三角形的高线是顶点到对边的距离;注意:三角形的中线和角平分线都在三角形内.