题目内容
如图,已知二次函数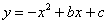
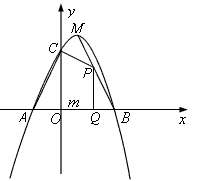
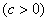 的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB=OC=3,顶点为M。
的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB=OC=3,顶点为M。
(1)求二次函数的解析式;
(2)点P为线段BM上的一个动点,过点P作x轴的垂线PQ,垂足为Q,若OQ=m,四边形ACPQ的面积为S,求S关于m的函数解析式,并写出m的取值范围;
(3)探索:线段BM上是否存在点N,使△NMC为等腰三角形;如果存在,求出点N的坐标;如果不存在,请说明理由。
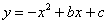
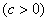 的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB=OC=3,顶点为M。
的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB=OC=3,顶点为M。(1)求二次函数的解析式;
(2)点P为线段BM上的一个动点,过点P作x轴的垂线PQ,垂足为Q,若OQ=m,四边形ACPQ的面积为S,求S关于m的函数解析式,并写出m的取值范围;
(3)探索:线段BM上是否存在点N,使△NMC为等腰三角形;如果存在,求出点N的坐标;如果不存在,请说明理由。
(1)∵OB=OC=3,∴B(3,0),C(0,3)
∴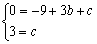 ,解得
,解得
∴二次函数的解析式为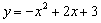 ;
;
(2) ,∴M(1,4)
,∴M(1,4)
设直线MB的解析式为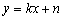 ,则有
,则有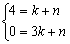 ,解得
,解得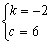
∴直线MB的解析式为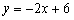
∵PQ⊥轴,OQ=m,∴点P的坐标为(m,-2m+6)

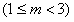
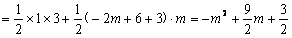
(3)线段BM上存在点N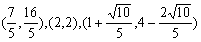 使△NMC为等腰三角形;
使△NMC为等腰三角形;
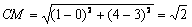 ,
,
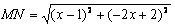
①当CM=NC时,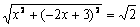 ,解得
,解得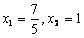 (舍去)
(舍去)
此时N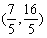
②当CM=MN时,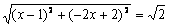
解得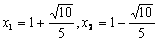 (舍去),此时N
(舍去),此时N 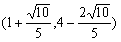
③当CN=MN时,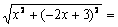
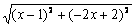
解得x=2,此时N (2,2)
∴
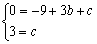 ,解得
,解得
∴二次函数的解析式为
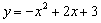 ;
;(2)
 ,∴M(1,4)
,∴M(1,4)设直线MB的解析式为
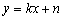 ,则有
,则有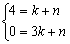 ,解得
,解得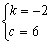
∴直线MB的解析式为
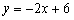
∵PQ⊥轴,OQ=m,∴点P的坐标为(m,-2m+6)

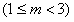
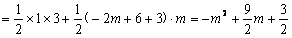
(3)线段BM上存在点N
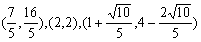 使△NMC为等腰三角形;
使△NMC为等腰三角形;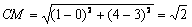 ,
,
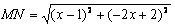
①当CM=NC时,
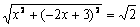 ,解得
,解得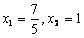 (舍去)
(舍去)此时N
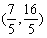
②当CM=MN时,
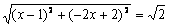
解得
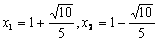 (舍去),此时N
(舍去),此时N 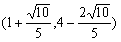
③当CN=MN时,
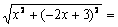
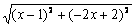
解得x=2,此时N (2,2)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的一个动点,过点P作x轴的垂线,垂足为D(m,0),并与直线OA交于点C.
的一个动点,过点P作x轴的垂线,垂足为D(m,0),并与直线OA交于点C. (2013•呼和浩特)如图,已知二次函数的图象经过点A(6,0)、B(-2,0)和点C(0,-8).
(2013•呼和浩特)如图,已知二次函数的图象经过点A(6,0)、B(-2,0)和点C(0,-8).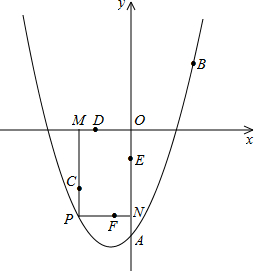 (2013•常德)如图,已知二次函数的图象过点A(0,-3),B(
(2013•常德)如图,已知二次函数的图象过点A(0,-3),B( 如图,已知二次函数的图象与x轴交于A(2,0)、B(6,0)两点,与y轴交于点D(0,4).
如图,已知二次函数的图象与x轴交于A(2,0)、B(6,0)两点,与y轴交于点D(0,4). 如图,已知二次函数的图象(0≤x≤3.4),关于该函数在所给自变量的取值范围内,下列说法正确的是( )
如图,已知二次函数的图象(0≤x≤3.4),关于该函数在所给自变量的取值范围内,下列说法正确的是( )