��Ŀ����
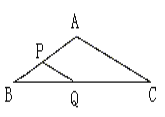
����Ŀ����������������1����ͼ1��ͼ�����ǰ�����Ϊ��8����������˵����A+��B=��C+��D��
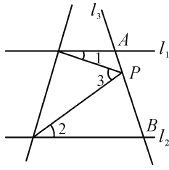
��2���Ķ���������������������������� ��ͼ2��AP��CP�ֱ�ƽ����BAD����BCD������ABC=36������ADC=16��������P�Ķ�����
������AP��CP�ֱ�ƽ����BAD����BCD
���1=��2����3=��4
�ɣ�1���Ľ��۵�����P+��3=��1+��B������P+��2=��4+��D������+������2��P+��2+��3=��1+��4+��B+��D
���P= ![]() ����B+��D��=26����
����B+��D��=26����
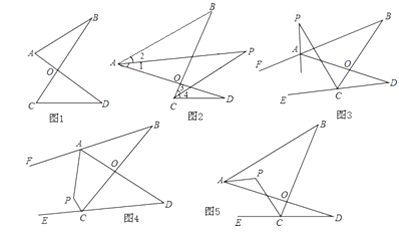
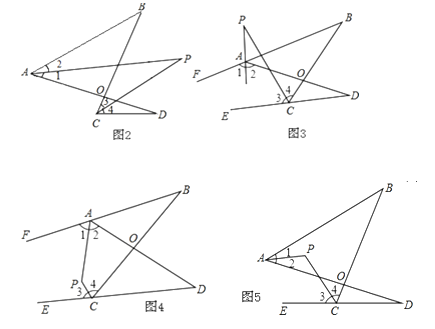
����ͼ3��ֱ��APƽ����BAD�������FAD��CPƽ����BCD�������BCE������ABC=36������ADC=16�����������P�Ķ�������˵��������
����ͼ4����ֱ��APƽ����BAD�������FAD��CPƽ����BCD�������BCE��������P����B����D�Ĺ�ϵ��ֱ��д������������˵��������
����ͼ5����APƽ����BAD��CPƽ����BCD�������BCE��������P����B����D�Ĺ�ϵ��ֱ��д������������˵��������
���𰸡���1��֤������������2������P=26�b������P=180����![]() ����B+��D��������P=90��+
����B+��D��������P=90��+ ![]() ����B+��D����
����B+��D����
�������������������1�����������ε��ڽǺ͵���180����ʽ�������ɵ�֤��
��2�����ݽ�ƽ���ߵĶ���ɵ���1=��2����3=��4���ٸ��ݣ�1���Ľ����г��������ɵý⣻����ʾ����PAD����PCD���ٸ��ݣ�1���Ľ����г���ʽ���������ɵý⣻
�������ı��ε��ڽǺ͵���360�����ɵã�180�㩁��1��+��P+��4+��B=360������2+��P+��180�㩁��3��+��D=360����Ȼ���������ɵý⣻
�����ݣ�1���Ľ�����B+��BAD=��D+��BCD����PAD+��P=��D+��PCD��Ȼ���������ɵý⣮
�����������1���ߡ�A+��B+��AOB=180������C+��D+��COD=180�b�� ���A+��B+��AOB=��C+��D+��COD���ߡ�AOB=��COD�����A+��B=��C+��D��
��2���١�P=26�b����APƽ����BAD�������FAD��CPƽ����BCD�������BCE�����1=��2����3=��4���ɣ�1���Ľ��۵ã���PAD+��P=��PCD+��D ������PAB+��P=��PCB+��B �����ߡ�PAB=��1����1=��2�����PAB=��2�����2+��P=��3+��B ������+������2+��P+��PAD+��P=��3+��B+��PCD+��D����2��P+180��=��B+��D+180�������P=![]() ����B+��D ��=26����
����B+��D ��=26����
����ͼ4����APƽ����BAD�������FAD��CPƽ����BCD�������BCE�����1=��2����3=��4������180����2��1��+��B=��180����2��4��+��D�����ı���APCB�У���180������1��+��P+��4+��B=360�������ı���APCD�У���2+��P+��180������3��+��D=360������2��P+��B+��D=360�������P=180����![]() ����B+��D����
����B+��D����
����ͼ5����APƽ����BAD��CPƽ����BCD�������BCE�����1=��2����3=��4��������1+��2��+��B=��180����2��3��+��D����2+��P=��180������3��+��D��![]() ����B+��D����
����B+��D����

 ���Ž�������С״Ԫϵ�д�
���Ž�������С״Ԫϵ�д�