题目内容
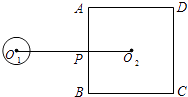
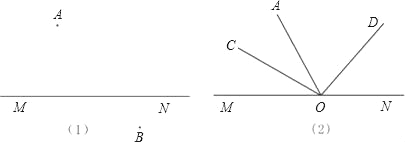
【题目】(1)如图(1),已知A、B位于直线MN的两侧,请在直线MN上找一点P,使PA+PB最小,并说明依据.
(2)如图(2),动点O在直线MN上运动,连接AO,分别画∠AOM、∠AON的角平分线OC、OD,请问∠COD的度数是否发生变化?若不变,求出∠COD的度数;若变化,说明理由.
【答案】(1)见解析;(2)∠COD的度数不会变化,为90°.
【解析】
(1)根据两点之间,线段最短,连接A、B两点与直线的交点即为所求作的点;
(2)根据角平分线的概念以及平角的概念进行求解即可.
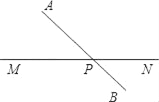
(1)如图,连接AB交MN于点P,则P就是所求的点,
理由:两点之间,线段最短;
(2)∠COD的度数不会变化,
∵OC是∠AOM的平分线,
∴∠COA=![]() ∠AOM,
∠AOM,
∵OD是∠AON的平分线,
∴∠AOD=![]() ∠AON,
∠AON,
∵∠AOM+∠AON=180°,
∴∠COD=∠COA+∠AOD=![]() ∠AOM+
∠AOM+![]() ∠AON=
∠AON=![]() (∠AOM+∠AON)=90°.
(∠AOM+∠AON)=90°.

练习册系列答案
相关题目