题目内容
【题目】如图,在△ABC中E是BC上的一点,EC=2EB,点D是AC的中点,AE、BD交于点F,AF=3FE.若△ABC的面积为18,给出下列命题: ①△ABE的面积为6;
②△ABF的面积和四边形DFEC的面积相等;
③点F是BD的中点;
④四边形DFEC的面积为 ![]() .
.
其中,正确的结论有 . (把你认为正确的结论的序号都填上)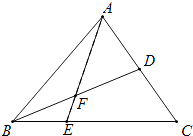
【答案】①③④
【解析】解:①∵△ABC的面积为18,EC=2EB, ∴△ABE的面积=18× ![]() =6,故①正确;
=6,故①正确;
②∵EC=2EB,点D是AC的中点,
∴△ABE的面积≠△BCD的面积,
∴△ABF的面积和四边形DFEC的面积不相等,故②错误;
③过D点作DG∥BC,
∵点D是AC的中点,
∴DG= ![]() EC,
EC,
∵EC=2EB,
∴DG=BE,
∵DG∥BC,
∴∠DGF=∠BEF,∠GDF=∠EBF,
在△DGF与△BEF中, ,
,
∴△DGF≌△BEF(ASA),
∴DF=BF,
∴点F是BD的中点,故③正确;
④四边形DFEC的面积=18﹣18× ![]() ﹣18×
﹣18× ![]() ×
× ![]()
=18﹣6﹣ ![]()
= ![]() ,故④正确.
,故④正确.
故正确的结论有①③④.
所以答案是:①③④.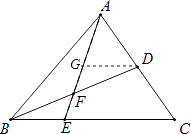
【考点精析】本题主要考查了三角形的面积的相关知识点,需要掌握三角形的面积=1/2×底×高才能正确解答此题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目