题目内容
 如图,AD为△ABC的中线,BE为△ABD的中线.
如图,AD为△ABC的中线,BE为△ABD的中线.(1)已知AB-AC=5cm,△ABD的周长为25cm,求△ADC的周长;
(2)在△AEB中作AE边上的高;
(3)若△ABC的面积为40,AE=5,则点B到AE边的距离为多少?
分析:(1)根据中线的定义可得BD=CD,然后表示出△ABD的周长,再把AB用AC表示,BD用CD表示,整理即可得解;
(2)根据三角形高线的定义作出即可;
(3)根据等底等高的三角形的面积相等用△ABC的面积表示出△ABE的面积,再利用三角形的面积公式列式计算即可得解.
(2)根据三角形高线的定义作出即可;
(3)根据等底等高的三角形的面积相等用△ABC的面积表示出△ABE的面积,再利用三角形的面积公式列式计算即可得解.
解答: 解:(1)∵AD为△ABC的中线,
解:(1)∵AD为△ABC的中线,
∴BD=CD,
∵AB-AC=5cm,
∴AB=AC+5,
△ABD的周长=AB+AD=BD=25,
即AC+5+AD+CD=25,
整理得,AC+AD+CD=25-5=20,
所以,△ADC的周长为20cm;
(2)如图所示,BF即为△AEB中AE边上的高;
(3)∵AD为△ABC的中线,BE为△ABD的中线,
∴S△ABD=
S△ABC,S△ABE=
S△ABD,
∴S△ABE=
S△ABC,
∵△ABC的面积为40,
∴△ABE的面积为
×40=10,
设点B到AE边的距离为h,
∵AE=5,
∴
×AE×h=10,
即
×5×h=10,
解得h=4.
故答案为:4.
 解:(1)∵AD为△ABC的中线,
解:(1)∵AD为△ABC的中线,∴BD=CD,
∵AB-AC=5cm,
∴AB=AC+5,
△ABD的周长=AB+AD=BD=25,
即AC+5+AD+CD=25,
整理得,AC+AD+CD=25-5=20,
所以,△ADC的周长为20cm;
(2)如图所示,BF即为△AEB中AE边上的高;
(3)∵AD为△ABC的中线,BE为△ABD的中线,
∴S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△ABE=
| 1 |
| 4 |
∵△ABC的面积为40,
∴△ABE的面积为
| 1 |
| 4 |
设点B到AE边的距离为h,
∵AE=5,
∴
| 1 |
| 2 |
即
| 1 |
| 2 |
解得h=4.
故答案为:4.
点评:本题考查了三角形的面积,三角形的中线、高线,解决此类题目最常用的是等底等高的三角形的面积相等,要熟练掌握.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
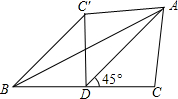 如图,AD为△ABC的中线,∠ADC=45°,把△ADC沿AD对折,点C落在点C′的位置,BC=4,求BC′的长.
如图,AD为△ABC的中线,∠ADC=45°,把△ADC沿AD对折,点C落在点C′的位置,BC=4,求BC′的长.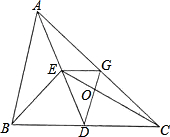 如图,AD为△ABC的中线,BE为△ABD的中线.
如图,AD为△ABC的中线,BE为△ABD的中线.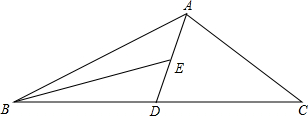 如图,AD为△ABC的中线,BE为三角形ABD中线,
如图,AD为△ABC的中线,BE为三角形ABD中线, 如图,AD为△ABC的中线,BE为△ABD的中线.
如图,AD为△ABC的中线,BE为△ABD的中线.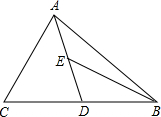 如图,AD为△ABC的中线,BE为△ABD的中线.
如图,AD为△ABC的中线,BE为△ABD的中线.