题目内容
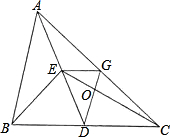 如图,AD为△ABC的中线,BE为△ABD的中线.
如图,AD为△ABC的中线,BE为△ABD的中线.(1)在△BED中作BD边上的高,垂足为F;
(2)若△ABC的面积为20,BD=5.
①△ABD的面积为
②求△BDE中BD边上的高EF的长;
(3)过点E作EG∥BC,交AC于点G,连接EC、DG且相交于点O,若S△ABC=2m,又S△COD=n,求S△GOC.(用含m、n的代数式表示)
分析:(1)根据尺规作图,作出垂线EF,
(2)①三角形的中线将三角形的面积等分成两份,从而求得△ABD的面积;
②由S△ABD再求出三角形BDE的面积,则得BD边上的高;
③由平行线可得S△BDE=S△CDG=
S△ABD=
S△ABC,从而求得S△COG.
(2)①三角形的中线将三角形的面积等分成两份,从而求得△ABD的面积;
②由S△ABD再求出三角形BDE的面积,则得BD边上的高;
③由平行线可得S△BDE=S△CDG=
| 1 |
| 2 |
| 1 |
| 4 |
解答: 解:(1)作EF⊥BD垂足为F,
解:(1)作EF⊥BD垂足为F,
(2)①∵AD为△ABC的中线,
∴S△ABD=
S△ABC,
∵△ABC的面积为20,
∴△ABD的面积为10;
②∵BE为△ABD的中线,
∴S△BDE=
S△ABD=5,
∵BD=5,
∴EF的长=2;
③∵EG∥BC,BE为△ABD的中线,
∴EG是△ACD的中位线,
∴DG是△ACD的中线,
∴S△BDE=S△CDG,S△BDE=S△CDG=
S△ABD=
S△ABC=
×2m=
,
∴S△GDC=
,又∵S△COD=n,
∴S△GOC=S△GDC-S△COD=
-n.
 解:(1)作EF⊥BD垂足为F,
解:(1)作EF⊥BD垂足为F,(2)①∵AD为△ABC的中线,
∴S△ABD=
| 1 |
| 2 |
∵△ABC的面积为20,
∴△ABD的面积为10;
②∵BE为△ABD的中线,
∴S△BDE=
| 1 |
| 2 |
∵BD=5,
∴EF的长=2;
③∵EG∥BC,BE为△ABD的中线,
∴EG是△ACD的中位线,
∴DG是△ACD的中线,
∴S△BDE=S△CDG,S△BDE=S△CDG=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| m |
| 2 |
∴S△GDC=
| m |
| 2 |
∴S△GOC=S△GDC-S△COD=
| m |
| 2 |
点评:本题考查了一个很重要的知识点:三角形的中线将三角形分成两个三角形,它们的面积等于原三角形面积的一半.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案
相关题目
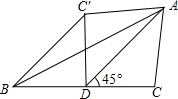 如图,AD为△ABC的中线,∠ADC=45°,把△ADC沿AD对折,点C落在点C′的位置,BC=4,求BC′的长.
如图,AD为△ABC的中线,∠ADC=45°,把△ADC沿AD对折,点C落在点C′的位置,BC=4,求BC′的长. 如图,AD为△ABC的中线,BE为三角形ABD中线,
如图,AD为△ABC的中线,BE为三角形ABD中线, 如图,AD为△ABC的中线,BE为△ABD的中线.
如图,AD为△ABC的中线,BE为△ABD的中线. 如图,AD为△ABC的中线,BE为△ABD的中线.
如图,AD为△ABC的中线,BE为△ABD的中线.