题目内容
已知A、B两地相距300千米,甲、乙两车同时从A地出发,以各自的速度匀速往返两地,甲车先到达B地,停留1小时后按原路返回.设两车行驶的时间为x小时,离开A地的距离是y千米,如图是y与x的函数图象.
(1)计算甲车的速度为 千米/时,乙车的速度为 千米/时;
(2)几小时后两车相遇;
(3)在从开始出发到两车相遇的过程中,设两车之间的距离为S千米,乙车行驶的时间为t小时,求S与t之间的函数关系式.
(1)100,60;(2)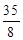 ;(3)当0≤t≤3时,S=40t;当3<t≤4时,S=300-60t;当4<t≤
;(3)当0≤t≤3时,S=40t;当3<t≤4时,S=300-60t;当4<t≤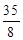 时,S=60-(60+100)(t-4)=700-160t.
时,S=60-(60+100)(t-4)=700-160t.
解析试题分析:(1)由图象直线的斜率能写出两车的速度,
(2)根据函数图象设出两线的关系式,列出两个函数解析式,联立求解,
(3)S与t之间的函数关系式是分段函数,在每个时间段中,求出两车的路程之差.
(1)甲车速度为100千米/小时;乙车速度为60千米/小时;
(2)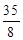 小时两车相遇.
小时两车相遇.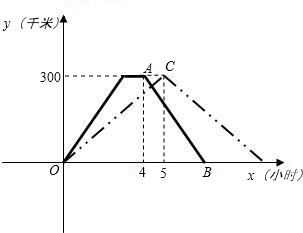
设OC的关系式为:y=kx,
∵图象经过(5,300),
∴300=5k,
k=60,
∴OC的关系式为:y=60x,
∵甲车速度为100千米/小时,
∴B(7,0),
设AB的关系式为y=kx+b,
∵图象经过A(4,300),B(7,0)
∴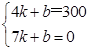 ,
,
解得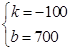 ,
,
∴AB的关系式为y=-100x+700,
联立两个函数关系式 ,解得x=
,解得x=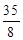 ;
;
(3)当0≤t≤3时,S=40t;当3<t≤4时,S=300-60t;当4<t≤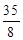 时,S=60-(60+100)(t-4)=700-160t.
时,S=60-(60+100)(t-4)=700-160t.
考点:一次函数的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某中学为了了解全校的耗电情况,抽查了10天中全校每天的耗电量,数据如下表:
| 千瓦时 | 90 | 93 | 102 | 113 | 114 | 120 |
| 天数 | 1 | 1 | 2 | 3 | 1 | 2 |
(2)根据上题获得的数据,估计该校一个月的耗电量(按30天计算).
(3)若当地每千瓦时电的价格是0.5元,写出该校应付电费y(元)与天数
 (
( 取正整数,单位:天)的函数关系式.
取正整数,单位:天)的函数关系式.  的图象相交于点A(a,1),求直线l的解析式.
的图象相交于点A(a,1),求直线l的解析式. 的图象与反比例函数
的图象与反比例函数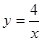 的图象交于点
的图象交于点 ,与
,与 轴交于点
轴交于点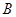 .
.
 的图像分别是
的图像分别是 ,半径为1的
,半径为1的 与直线
与直线 中的两条相切,例如
中的两条相切,例如 是其中一个
是其中一个

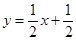 的图象与x轴交于点A,与y轴交于点B,与反比例函数
的图象与x轴交于点A,与y轴交于点B,与反比例函数 的图象在第一象限内交于点C,CD⊥x轴于点D,OD=2AO,求反比例函数
的图象在第一象限内交于点C,CD⊥x轴于点D,OD=2AO,求反比例函数 的表达式.
的表达式. 


 (x-2)2+m的x的取值范围.
(x-2)2+m的x的取值范围.