题目内容
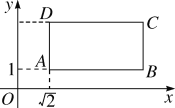
【题目】已知:如图,△ABC中,∠BAC=90°,点D在BC边上,且BD=BA,过点B画AD的垂线交AC于点O,以O为圆心,AO为半径画圆.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为8,tan∠C= ![]() ,求线段AB的长,sin∠ADB的值.
,求线段AB的长,sin∠ADB的值.
【答案】
(1)解:连接OD,
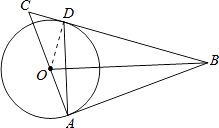
∵BA=BD,BO⊥AD,
∴∠ABO=∠DBO,
在△ABO和△DBO中,
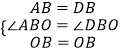 ,
,
∴△ABO≌△DBO(SAS),
∴OD=OA.∠ODB=∠OAB=90°,
∴BD⊥OD,
∴BC是⊙O的切线
(2)解:∵在RT△ODC中,CD= ![]() =6,
=6,
∴OC=10,
∴AC=18,
在RT△ABC中,AB=ACtan∠C=18× ![]() =24,
=24,
∵∠ADB=∠DAB=∠AOB,
∴sin∠ADB=sin∠AOB= ![]() =
= ![]()
【解析】(1)根据等腰三角形的性质三线合一,由SAS得到△ABO≌△DBO,得到BD⊥OD,得到BC是⊙O的切线;(2)根据三角函数值,求出OC、AC的值,根据三角函数值和勾股定理求出sin∠ADB的值.
【考点精析】解答此题的关键在于理解切线的判定定理的相关知识,掌握切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线,以及对解直角三角形的理解,了解解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目