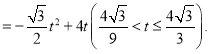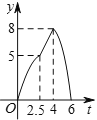题目内容
【题目】如图，抛物线y＝﹣
x2+bx+c经过点B（2
，0）、C（0，2）两点，与x轴的另一个交点为A．
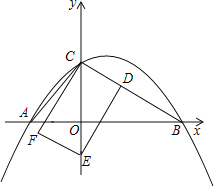
（1）求抛物线的解析式；
（2）点D从点C出发沿线段CB以每秒个单位长度的速度向点B运动，作DE⊥CB交y轴于点E，以CD、DE为边作矩形CDEF，设点D运动时间为t（s）．
①当点F落在抛物线上时，求t的值；
②若点D在运动过程中，设△ABC与矩形CDEF重叠部分的面积为S，请直接写出S与t之间的函数关系式，并写出自变量t的取值范围．
【答案】（1）
；（2）①
②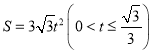
，
，
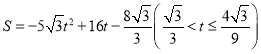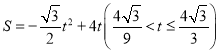
【解析】
（1）把B、C的坐标代入抛物线的解析式求解即可；
（2）①点F在抛物线上，作DG⊥y轴，FH⊥y轴，证明△CDG≌△EFH，根据全等三角形的性质有CG=HE，GD=FH，证明△CGD∽△COB，根据相似三角形的性质得到
表示出OH的长度，即可求得点F的坐标，最后将点F的坐标代入抛物线的解析式求解即可；
②当
时，S=CDDE；当
时，S=矩形DEGF的面积-△GEH的面积．当
时，
解：（1）把
两点代入抛物线解析式得：
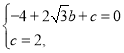
解得：
则抛物线解析式为
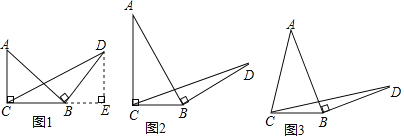
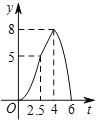
（2）①如图1所示，点F在抛物线上，作DG⊥y轴，FH⊥y轴，
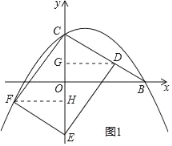
易得△CDG≌△EFH，即CG＝HE，GD＝FH，
由题意得：
∵△CGD∽△COB，
∴
即
∴OH＝
，即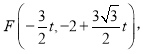
代入抛物线解析式得： 
解得：t=
；
②分三种情况考虑：
（i）如图2所示，△ABC与矩形CDEF重叠部分为矩形CDEF，
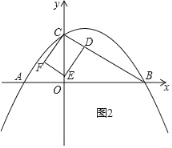
在Rt△CDE中，
∴DE＝3t，
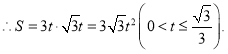
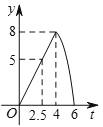
（ii）如图3所示，△ABC与矩形CDEF重叠部分为五边形CDHGF，
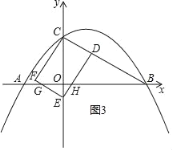
由题意得：
在Rt△CED中，∠ECD＝60°，
∴
∴
在Rt△OGE中，
同理可得
即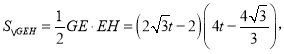
则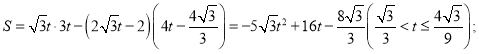
（iii）如图4，△ABC与矩形CDEF重叠部分为四边形CDMN，
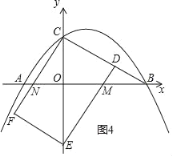
由题意得：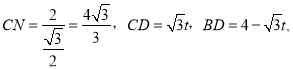 
在Rt△BMD中， 
则
，
