题目内容
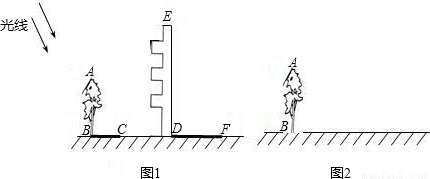
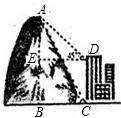
高为12.6米的教学楼ED前有一棵大树AB(如图1).(1)某一时刻测得大树AB、教学楼ED在阳光下的投影长分别是BC=2.4米,DF=7.2米,求大树AB的高度;
(2)用皮尺、高为h米的测角仪,请你设计另一种测量大树AB高度的方案,要求:①在图2上,画出你设计的测量方案示意图,并将应测数据标记在图上(长度用字母m、n …表示,角度用希腊字母α、β …表示);
②根据你所画的示意图和标注的数据,计算大树AB高度(用字母表示).
【答案】分析:(1)首先根据平行线的性质判断出△ABC∽△EDF;得到比例关系式,可求得AB的值;
(2)根据题意,设计测量方法,要求符合三角函数的定义,且易于操作即可.
解答: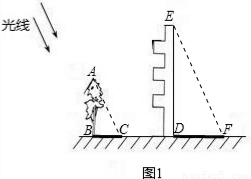 解:连接AC、EF,
解:连接AC、EF,
(1)∵太阳光线是平行线,
∴AC∥EF,
∴∠ACB=∠EFD.
∵∠ABC=∠EDF=90°,
∴△ABC∽△EDF,
∴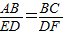 ∴
∴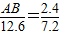 .
.
∴AB=4.2.
答:大树AB的高是4.2米.
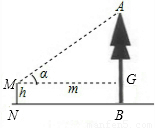
(2)(方法一)
如图,MG=BN=m,
AG=mtanα
∴AB=(mtanα+h)米
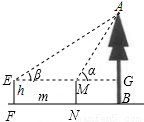 (方法二)
(方法二)
AG=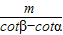
∴AB=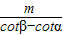 +h
+h
或AB=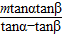 +h.
+h.
点评:本题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形.
(2)根据题意,设计测量方法,要求符合三角函数的定义,且易于操作即可.
解答:
 解:连接AC、EF,
解:连接AC、EF,(1)∵太阳光线是平行线,
∴AC∥EF,
∴∠ACB=∠EFD.
∵∠ABC=∠EDF=90°,
∴△ABC∽△EDF,
∴
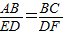 ∴
∴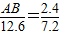 .
.∴AB=4.2.
答:大树AB的高是4.2米.

(2)(方法一)
如图,MG=BN=m,
AG=mtanα
∴AB=(mtanα+h)米
 (方法二)
(方法二)AG=
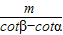
∴AB=
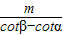 +h
+h或AB=
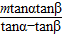 +h.
+h.点评:本题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
 精确到0.1米,化简后再代入参数数据运算)
精确到0.1米,化简后再代入参数数据运算)

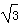 =1.73,
=1.73,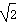 =1.41,精确到0.1米,化简后再代入参考数据运算)
=1.41,精确到0.1米,化简后再代入参考数据运算) 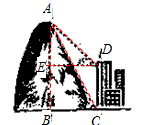
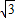 =1.73
=1.73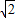 =1.41,精确到0.1米,化简后再代入参数数据运算)
=1.41,精确到0.1米,化简后再代入参数数据运算)