题目内容
某乡镇中学数学活动小组,为测量数学楼后面的山高AB,用了如下方法.如图所示,在教学楼底C处测得山顶A的仰角为60°,在教学楼顶D处,测得山顶A的俯角为45°.已知教学楼高CD=12米,求山高AB.(参考数据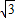 =1.73
=1.73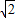 =1.41,精确到0.1米,化简后再代入参数数据运算)
=1.41,精确到0.1米,化简后再代入参数数据运算)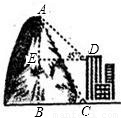
【答案】分析:过D作AB的垂线,设垂足为E.在Rt△ABC中,可用AB表示出BC的长,进而可在Rt△ADE中,表示出AE的长;
根据BE=AB-AE=12,即可求出山高AB的长度.
解答: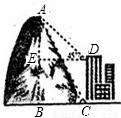 解:过D作DE⊥AB于E,则DE∥BC.
解:过D作DE⊥AB于E,则DE∥BC.
设AB=h米.
在Rt△ABC中,BC=h•cot60°=h•tan30°=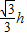 . (2分)
. (2分)
在Rt△AED中,AE=DEtan45°=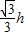 . (2分)
. (2分)
又AB-AE=BE=CD=12,
∴h-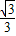 h=12,(2分)
h=12,(2分)
h=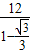 =
=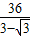 =
=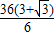
=18+6 =18+6×1.73
=18+6×1.73
=18+10.38≈28.4(米) (2分)
答:山高AB是28.4米. (1分)
点评:解直角梯形可以通过作高线转化为解直角三角形和矩形的问题.
根据BE=AB-AE=12,即可求出山高AB的长度.
解答:
 解:过D作DE⊥AB于E,则DE∥BC.
解:过D作DE⊥AB于E,则DE∥BC.设AB=h米.
在Rt△ABC中,BC=h•cot60°=h•tan30°=
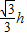 . (2分)
. (2分)在Rt△AED中,AE=DEtan45°=
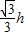 . (2分)
. (2分)又AB-AE=BE=CD=12,
∴h-
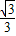 h=12,(2分)
h=12,(2分)h=
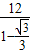 =
=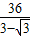 =
=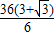
=18+6
 =18+6×1.73
=18+6×1.73=18+10.38≈28.4(米) (2分)
答:山高AB是28.4米. (1分)
点评:解直角梯形可以通过作高线转化为解直角三角形和矩形的问题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目



