题目内容
2、在四边形ABCD中,AC与BD相交于点O,如果只给出条件“AB∥CD”,那么还不能判定四边形ABCD为平行四边形,给出以下六个说法中,正确的说法有( )
(1)如果再加上条件“AD∥BC”,那么四边形ABCD一定是平行四边形;
(2)如果再加上条件“AB=CD”,那么四边形ABCD一定是平行四边形;
(3)如果再加上条件“∠DAB=∠DCB”那么四边形ABCD一定是平行四边形;
(4)如果再加上“BC=AD”,那么四边形ABCD一定是平行四边形;
(5)如果再加上条件“AO=CO”,那么四边形ABCD一定是平行四边形;
(6)如果再加上条件“∠DBA=∠CAB”,那么四边形ABCD一定是平行四边形.
(1)如果再加上条件“AD∥BC”,那么四边形ABCD一定是平行四边形;
(2)如果再加上条件“AB=CD”,那么四边形ABCD一定是平行四边形;
(3)如果再加上条件“∠DAB=∠DCB”那么四边形ABCD一定是平行四边形;
(4)如果再加上“BC=AD”,那么四边形ABCD一定是平行四边形;
(5)如果再加上条件“AO=CO”,那么四边形ABCD一定是平行四边形;
(6)如果再加上条件“∠DBA=∠CAB”,那么四边形ABCD一定是平行四边形.
分析:(1)因为两组对边分别平行的四边形是平行四边形,所以①正确;
(2)因为一组对边平行且相等的四边形是平行四边形,所以②正确;
(3)此题易证此四边形的两组对边分别平行,所以③正确;
(5)此题可以通过证明三角形全等,证得AB=CD,所以证得此四边形是平行四边形;正确;
(4)与(6)等腰梯形也符合要求,所以错误.
(2)因为一组对边平行且相等的四边形是平行四边形,所以②正确;
(3)此题易证此四边形的两组对边分别平行,所以③正确;
(5)此题可以通过证明三角形全等,证得AB=CD,所以证得此四边形是平行四边形;正确;
(4)与(6)等腰梯形也符合要求,所以错误.
解答:解: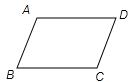 (1)∵AB∥CD,AD∥BC,
(1)∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形;正确;
(2)∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形;正确;
(3)∵AB∥CD,
∴∠A+∠D=180°,
∵∠DAB=∠DCB,
∴∠C+∠D=180°,
∴AD∥BC,
∴四边形ABCD是平行四边形;正确;
(4)可能是等腰梯形,所以错误;
(5)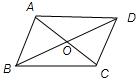
∵AB∥CD,
∴∠BAO=∠DCO,∠ABO=∠CDO,
∵AO=CO,
∴△AOB≌△COD,
∴AB=CD,
∴四边形ABCD是平行四边形;正确;
(6)此题可以是等腰梯形;错误.
故选C.
 (1)∵AB∥CD,AD∥BC,
(1)∵AB∥CD,AD∥BC,∴四边形ABCD是平行四边形;正确;
(2)∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形;正确;
(3)∵AB∥CD,
∴∠A+∠D=180°,
∵∠DAB=∠DCB,
∴∠C+∠D=180°,
∴AD∥BC,
∴四边形ABCD是平行四边形;正确;
(4)可能是等腰梯形,所以错误;
(5)

∵AB∥CD,
∴∠BAO=∠DCO,∠ABO=∠CDO,
∵AO=CO,
∴△AOB≌△COD,
∴AB=CD,
∴四边形ABCD是平行四边形;正确;
(6)此题可以是等腰梯形;错误.
故选C.
点评:此题考查了平行四边形的判定.注意真命题需要证明,假命题只要举反例即可.解题时还要注意数形结合思想的应用.

练习册系列答案
相关题目
 11、如图所示,在四边形ABCD中,BD是它的一条对角线,若∠1=∠2,∠A=55°16′,则∠ADC=
11、如图所示,在四边形ABCD中,BD是它的一条对角线,若∠1=∠2,∠A=55°16′,则∠ADC=
 如图,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是边DC的中点,N是边AB的中点.△MPN是什么三角形?为什么?
如图,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是边DC的中点,N是边AB的中点.△MPN是什么三角形?为什么?