Question

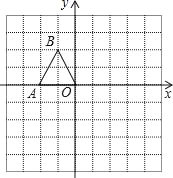
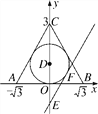
【题目】(2016·衡阳中考)如图，在平面直角坐标系中，△ABC三个顶点坐标为A(－，0)，B(，0)，C(0，3)．

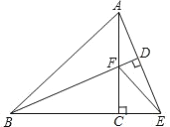
(1)求△ABC内切圆⊙D的半径；

(2)过点E(0，－1)的直线与⊙D相切于点F(点F在第一象限)，求直线EF的解析式．

Answer 1

【答案】（1）1；（2）y＝x－1.

【解析】试题分析：（1）连接BD，利用三角函数求得∠CBO，BD平分∠CBO，求出OD.

(2) )连接DF，过点F作FG⊥y轴于点G,利用三角函数求出∠DFG，解Rt△DGF，求出F点坐标，E坐标，求出直线EF解析式.

试题解析：

解：(1)连接BD.∵B点坐标为(，0)，C点坐标为(0，3)，∴OB＝，OC＝3，∴tan∠CBO＝＝，

∴∠CBO＝60°.∵点D是△ABC的内心，

∴BD平分∠CBO，∴∠DBO＝30°，

∴OD＝OB·tan30°＝1，即△ABC内切圆⊙D的半径为1；

(2)连接DF，过点F作FG⊥y轴于点G.

∵E点坐标为(0，－1)，

∴OE＝1，DE＝2.∵直线EF与⊙D相切，

∴∠DFE＝90°，DF＝1，∴sin∠DEF＝＝

∴∠DEF＝30°，

∴∠GDF＝60°，∠DFG＝30°.

在Rt△DGF中，∵∠DFG＝30°，∴DG＝DF＝，GF＝，

∴点F的坐标为().设直线EF的解析式为y＝kx＋b，代入点E，F的坐标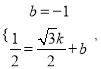得解得.

∴直线EF的解析式为y＝x－1.