题目内容
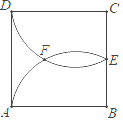
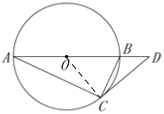
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,过点C作⊙O的切线,交直径AB的延长于点D,若∠ABC=65°,则∠D的度数是( )

A.25°B.30°C.40°D.50°
【答案】C
【解析】
如图,连接OC,根据切线的性质可得∠OCD=90°,根据AB是直角可得∠ACB=90°,根据角的和差关系可得∠BCD=∠CAB,根据直角三角形两锐角互余的性质可求出∠CAB的度数,利用三角形外角性质即可求出∠D的度数.
如图,连接OC,
∵CD是⊙O的切线,
∴∠OCD=90°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠ABC=65°,
∴∠CAB=90°-∠ABC=25°,
∵∠OCA+∠OCB=∠BCD+∠OCB=90°,
∴∠BCD=∠OCA,
∵OA=OC,
∴∠OCA=∠CAB,
∴∠BCD=∠CAB=25°,
∴∠D=∠ABC-∠BCD=40°,
故选:C.

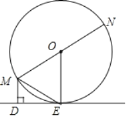
【题目】某公司招聘一名职员,先对应聘者进行笔试考核,笔试进入前两名的选手再进入面试方面的考核,最终在参加面试的两人中录取一人.该公司将应聘者的笔试成绩划分了4个等级:设应聘者的成绩为x(单位:分),当60≤x<70时为不合格;当70≤x<80时为合格;当80≤x<90时为良好;当90≤x≤100时为优秀.下面是参加笔试的10名应聘者的成绩:86 75 67 86 92 75 82 90 86 78
(1)这10名应聘者的笔试成绩的中位数是_______,众数是_______;
(2)请将下面表示上述4个等级的统计图补充完整;
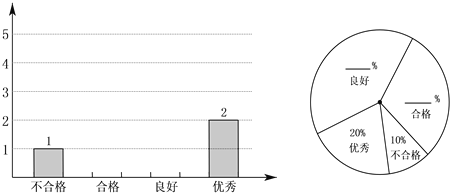
(3)该公司对进入笔试前两名的甲、乙二人进行了面试考核,面试中包括形体、口才、人际交往、创新能力,他们的成绩(百分制)如下表:
候选人 | 面试项目 | |||
形体 | 口才 | 人际交往 | 创新能力 | |
甲 | 86 | 90 | 95 | 90 |
乙 | 95 | 85 | 90 | 92 |
如果公司根据经营性质和岗位要求,以面试成绩中形体占10%,口才占20%,人际交往40%,创新能力占30%确定成绩,那么你认为该公司应该录取谁?请通过计算说明理由.