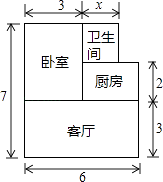
题目内容
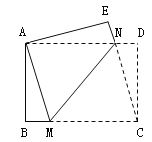
【题目】如图,在矩形ABCD中,AD>AB,将矩形ABCD折叠,使点C与点A重合,折痕为MN,连接CN.若△CDN的面积与△CMN的面积比为1:3,则![]() 的值为______________.
的值为______________.
【答案】12
【解析】如图,过点N作NG⊥BC于点G,连接CN,根据轴对称的性质有:
MA=MC,NA=NC,∠AMN=∠CMN.
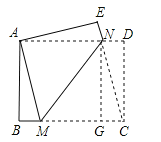
因为四边形ABCD是矩形,所以AD∥BC,所以∠ANM=∠CMN.
所以∠AMN=∠ANM,所以AM=AN.
所以AM=AN=CM=CN.
因为△CDN的面积与△CMN的面积比为1:3,所以DN:CM=1:3.
设DN=x,则CG=x,AM=AN=CM=CN=3x,
由勾股定理可得NG= ![]() ,
,
所以MN2=![]() ,BM2=
,BM2=![]() .
.
所以![]() =12.
=12.
枚本题应填12.

练习册系列答案
相关题目