Question

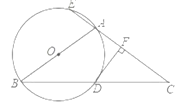
【题目】如图，Rt△ABC中，∠ACB=90°，∠ABC=30°，AC=4,D为线段AB上一个动点，以BD为边在△ABC外作等边三角形BDE。若F为DE的中点，则CF的最小值为 。

Answer 1

【答案】6
【解析】如下图：过点D作DGBC于点G，过点F作FHBC于点H，设等边EDB的边长为x，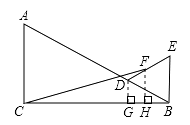

∵在RtDGB中，∠ABC=30°，∴DG=x，BG=x，
∵EDB是等边三角形，∴∠EBD=60°，∴∠EBC=90°，
∵点F是DE的中点，且FHDGEB，
∴点F也是GB的中点，即FH是梯形DGBE的中位线，
∴FH=（x+x）=x.
在RtABC中，∠ABC=30°，AC=4，
∴AB=8，BC=.
又∵BH=BG=x，
∴CH=-x，
在RtFCH中，CF2=FH2+CH2=（x）2+（-x）2=x2-6x+48=（x-4）2+36，
∵点D为线段AB上一个动点，∴0<x<8，
∴当x=4时，CF2=（x-4）2+36有最小值36，即CF的最小值为6.
故答案为：6.
设等边EDB的边长为x，过点D作DGBC于点G，过点F作FHBC于点H，在RtDGB中，用含x的代数式解出DG和BG；根据点F是DE的中点，且FHDGEB，判断出FH是梯形DGBE的中位线，进而求出FH的长；最后根据勾股定理表示出CF2的长，利用二次函数的最值求出CF2的最小值，进而求得CF的最小值.