题目内容
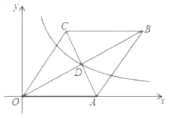
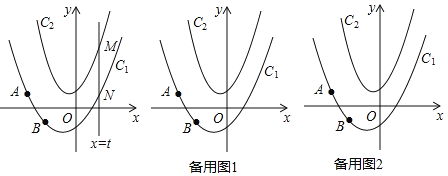
【题目】如图，在平面直角坐标系中，抛物线C1：y＝ax2+bx﹣1经过点A（﹣2，1）和点B（﹣1，﹣1），抛物线C2：y＝2x2+x+1，动直线x＝t与抛物线C1交于点N，与抛物线C2交于点M．
（1）求抛物线C1的表达式；
（2）当△AMN是以MN为直角边的等腰直角三角形时，求t的值；
（3）在（2）的条件下，设抛物线C1与y轴交于点P，点M在y轴右侧的抛物线C2上，连接AM交y轴于点K，连接KN，在平面内有一点Q，连接KQ和QN，当KQ＝1且∠KNQ＝∠BNP时，请直接写出点Q的坐标．
【答案】（1）y＝x2+x﹣1；（2）t的值为1或0；（3）满足条件的Q点坐标为：（0，2）、（﹣1，3）、（
，
）、（
，
）．
【解析】
（1）用待定系数法即可确定函数解析式；
（2）根据图形分∠ANM=90°和∠AMN=90°两种情况解答即可；
（3）根据题意画出满足条件图形，可以找到AN为△KNP对称轴，由对称性找到第一个满足条件Q，再通过延长和圆的对称性找到剩余三个点，利用勾股定理进行计算．
（1）∵抛物线C1：y＝ax2+bx﹣1经过点A（﹣2，1）和点B（﹣1，﹣1）
∴
解得：
∴抛物线C1：解析式为y＝x2+x﹣1
（2）∵动直线x＝t与抛物线C1交于点N，与抛物线C2交于点M
∴点N的纵坐标为t2+t﹣1，点M的纵坐标为2t2+t+1
∴MN＝（2t2+t+1）﹣（t2+t﹣1）＝t2+2
①当∠ANM＝90°，AN＝MN时，由已知N（t，t2+t﹣1），A（﹣2，1）
∴AN＝t﹣（﹣2）＝t+2
∵MN＝t2+2
∴t2+2＝t+2
∴t1＝0（舍去），t2＝1
∴t＝1
②当∠AMN＝90°，AM＝MN时，由已知M（t，2t2+t+1），A（﹣2，1）
∴AM＝t﹣（﹣2）＝t+2，
∵MN＝t2+2
∴t2+2＝t+2
∴t1＝0，t2＝1（舍去）
∴t＝0
故t的值为1或0；
（3）由（2）可知t＝1时M位于y轴右侧，根据题意画出示意图如图：
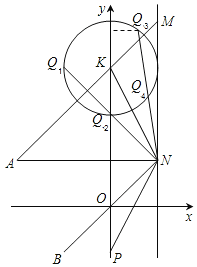
易得K（0，3），B、O、N三点共线
∵A（﹣2，1），N（1，1），P（0，﹣1）
∴点K、P关于直线AN对称
设半径为1的⊙K与y轴下方交点为Q2，则其坐标为（0，2）
∴Q2与点O关于直线AN对称
∴Q2是满足条件∠KNQ＝∠BNP．
则NQ2延长线与⊙K交点Q1，Q1、Q2关于KN的对称点Q3、Q4也满足∠KNQ＝∠BNP．
由图形易得Q1（﹣1，3）
设点Q3坐标为（m，n），由对称性可知Q3N＝NQ1＝BN＝
，
∵⊙K半径为1
∴
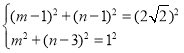
解得
或
．
同理，设点Q4坐标为（m，n），由对称性可知Q4N＝NQ2＝NO＝
，
∴
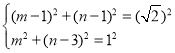
解得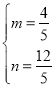
或
．
∴满足条件的Q点坐标为：（0，2）、（﹣1，3）、（，）、（，）．
