题目内容
 20、已知:抛物线y=x2+4x+3与x轴相交于A、B两点(A点在B点的左侧),顶点为P.
20、已知:抛物线y=x2+4x+3与x轴相交于A、B两点(A点在B点的左侧),顶点为P.(1)求A、B、P三点坐标;
(2)画出此抛物线的简图,并根据简图直接写出当-3<x<0时,函数值y的取值范围.
分析:(1)令x2+4x+3=0,求出方程的解即可得到方程与x轴的交点坐标;利用顶点坐标公式即可求出顶点P的坐标;
(2)画出图形即可观察出y的取值范围.
(2)画出图形即可观察出y的取值范围.
解答:解:(1)令x2+4x+3=0,
即(x+1)(x+3)=0,
解得x=-1,x=-3.
故A(-3,0),B(-1,0);
因为y=x2+4x+3=x2+4x+4-1=(x+2)2-1,
故顶点坐标为P(-2,-1).
(2)如图
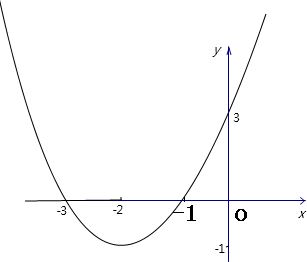
当-3<x<0时,-1<y<3.
即(x+1)(x+3)=0,
解得x=-1,x=-3.
故A(-3,0),B(-1,0);
因为y=x2+4x+3=x2+4x+4-1=(x+2)2-1,
故顶点坐标为P(-2,-1).
(2)如图

当-3<x<0时,-1<y<3.
点评:此题考查了抛物线与x轴的交点坐标,要转化为一元二次方程解得问题来解答,同时要注意数形结合.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目