题目内容
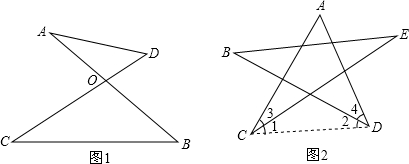
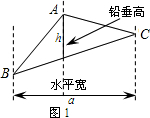
阅读材料:如图,△ABC中,AB=AC,P为底边BC上任意一点,点P到两腰的距离分别为r1,r2,腰上的高为h,连接AP,则S△ARP+S△ACP=S△ABC,即:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(1)理解与应用:
如图,在边长为3的正方形ABCD中,点E为对角线BD上的一点,且BE=BC,F为CE上一点,FM⊥BC于M,FN⊥BD于N,试利用上述结论求出FM+FN的长.
(2)类比与推理:
如果把“等腰三角形”改成“等边三角形”,那么P的位置可以由“在底边上任一点”放宽为“在三角形内任一点”,即:
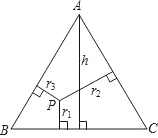
已知等边△ABC内任意一点P到各边的距离分别为r1,r2,r3,等边△ABC的高为h,试证明r1+r2+r3=h(定值).
(3)拓展与延伸:
若正n边形A1A2…An,内部任意一点P到各边的距离为r1r2…rn,请问r1+r2+…+rn是否为定值?如果是,请合理猜测出这个定值.
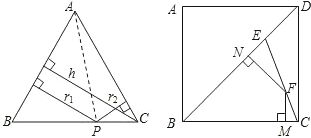
分析:(1)已知BE=BC,采用面积分割法,S△BFE+S△BCF=S△BEC得出三角形高的数量关系.
(2)连接PA,PB,PC,仿照面积的割补法,得出S△PBC+S△PAC+S△PAB=S△ABC,而这几个三角形的底相等,故可得出高的关系.
(3)问题转化为正n边形时,根据正n边形计算面积的方法,从中心向各顶点连线,可得出n个全等的等腰三角形,用边长为底,边心距为高,可求正n边形的面积,然后由P点向正n多边形,又可把正n边形分割成n过三角形,以边长为底,以r1r2…rn为高表示面积,列出面积的等式,可求证r1+r2+…+rn为定值.
(2)连接PA,PB,PC,仿照面积的割补法,得出S△PBC+S△PAC+S△PAB=S△ABC,而这几个三角形的底相等,故可得出高的关系.
(3)问题转化为正n边形时,根据正n边形计算面积的方法,从中心向各顶点连线,可得出n个全等的等腰三角形,用边长为底,边心距为高,可求正n边形的面积,然后由P点向正n多边形,又可把正n边形分割成n过三角形,以边长为底,以r1r2…rn为高表示面积,列出面积的等式,可求证r1+r2+…+rn为定值.
解答: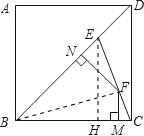 解:(1)过E点作EH⊥BC,垂足为H,连接BF,
解:(1)过E点作EH⊥BC,垂足为H,连接BF,
∵BE=BC=3,∠EBH=45°,
∴EH=
,
∵S△BFE+S△BCF=S△BEC,
∴
BE×FN+
BC×FM=
BC×EH,
∵BE=BC,
∴FN+FM=EH=
.
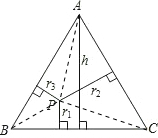
(2)连接PA,PB,PC,
∵S△PBC+S△PAC+S△PAB=S△ABC,
∴
BC•r1+
AC•r2+
AB•r3=
BC•h,
∵BC=AC=AB,
∴r1+r2+r3=h.
(3)设n边形的边心距为r,则:r1+r2+…+rn=nr(定值).
 解:(1)过E点作EH⊥BC,垂足为H,连接BF,
解:(1)过E点作EH⊥BC,垂足为H,连接BF,∵BE=BC=3,∠EBH=45°,
∴EH=
3
| ||
| 2 |
∵S△BFE+S△BCF=S△BEC,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵BE=BC,
∴FN+FM=EH=
3
| ||
| 2 |

(2)连接PA,PB,PC,
∵S△PBC+S△PAC+S△PAB=S△ABC,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵BC=AC=AB,
∴r1+r2+r3=h.
(3)设n边形的边心距为r,则:r1+r2+…+rn=nr(定值).
点评:本题主要利用面积分割法,求线段之间的关系,充分体现了面积法解题的作用.

练习册系列答案
相关题目


 阅读材料:
阅读材料: