题目内容
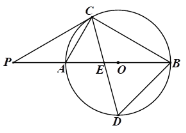
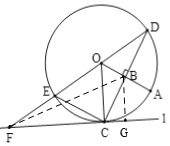
【题目】如图,B是![]() 的半径OA上的一点(不与端点重合),过点B作OA的垂线交
的半径OA上的一点(不与端点重合),过点B作OA的垂线交![]() 于点C,D,连接OD,E是
于点C,D,连接OD,E是![]() 上一点,
上一点,![]() ,过点C作
,过点C作![]() 的切线l,连接OE并延长交直线l于点F.
的切线l,连接OE并延长交直线l于点F.
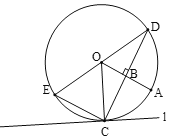
(1)①依题意补全图形.
②求证:∠OFC=∠ODC.
(2)连接FB,若B是OA的中点,![]() 的半径是4,求FB的长.
的半径是4,求FB的长.
【答案】(1)①补图见解析;②证明见解析;(2)FB=![]() .
.
【解析】
(1)①根据题意,补全图形即可;
②由CD⊥OA可得∠ODC+∠AOD=90°,根据垂径定理可得![]() ,利用等量代换可得
,利用等量代换可得![]() ,根据圆周角定理可得∠EOC=∠AOD,由切线性质可得OC⊥FC,可得∠OFC+∠FOC=90°,即可证明∠OFC=∠ODC;
,根据圆周角定理可得∠EOC=∠AOD,由切线性质可得OC⊥FC,可得∠OFC+∠FOC=90°,即可证明∠OFC=∠ODC;
(2)连接BF,作BG⊥l于G,根据OB=![]() OA,可得∠OCB=30°,利用勾股定理可求出BC的长,根据垂径定理可得CD的长,由(1)可知∠OFC=∠ODC,可得FC=CD,由BG⊥l,OC⊥l可得OC//BG,根据平行线的性质可得∠CBG=30°,根据含30°角的直角三角形的性质可求出CG的长,利用勾股定理可求出BG的长,即可求出FG的长,利用勾股定理求出FB的长即可.
OA,可得∠OCB=30°,利用勾股定理可求出BC的长,根据垂径定理可得CD的长,由(1)可知∠OFC=∠ODC,可得FC=CD,由BG⊥l,OC⊥l可得OC//BG,根据平行线的性质可得∠CBG=30°,根据含30°角的直角三角形的性质可求出CG的长,利用勾股定理可求出BG的长,即可求出FG的长,利用勾股定理求出FB的长即可.
(1)①延长OE,交直线l于F,如图即为所求,
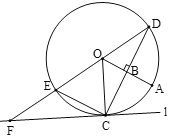
②∵OA⊥CD,OA为⊙O半径,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴∠EOC=∠AOD,
∵FC是⊙O的切线,
∴OC⊥FC,
∴∠OFC+∠FOC=90°,
∴∠OFC=∠ODC.
(2)连接BF,作BG⊥l于G,
∵B是OA的中点,⊙O半径为4,
∴OB=![]() OA=
OA=![]() OC=2,
OC=2,
∵OA⊥CD,
∴∠OCD=30°,BC=![]() =
=![]() =
=![]() ,
,
∴CD=2BC=![]() ,
,
由(1)可知∠OFC=∠ODC,
∴FC=CD=![]() ,
,
∵BG⊥l,OC⊥l,
∴OC//BG,
∴∠CBG=∠OCD=30°,
∴CG=![]() BC=
BC=![]() ,BG=
,BG=![]() =3,
=3,
∴FG=FC+CG=![]() ,
,
∴BF=![]() =
=![]() .
.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目