题目内容
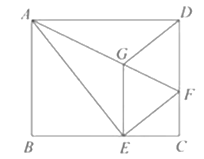
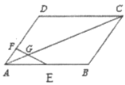
【题目】如图,在![]() 中,E为AB的中点,F为AD上一点,EF交AC于点G,
中,E为AB的中点,F为AD上一点,EF交AC于点G,![]() ,
,![]() ,
,![]() ,则AC的长为___.
,则AC的长为___.
【答案】30 cm
【解析】
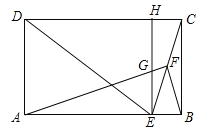
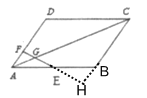
延长FG交CB的延长线于点H,根据平行四边形的性质,得BC=AD=12cm,BC∥AD,根据AAS可以证明△AFE≌△BHE,则BH=AF=4cm,再根据BC∥AD,利用平行线分线段成比例定理,求得CG的长,从而求得AC的长.
解:延长FG交CB的延长线于点H,
∵四边形ABCD是平行四边形,
∴BC=AD=8+4=12cm,BC∥AD,
∴∠EAF=∠EBH,∠AFE=∠BHE,
在△AFE与△BHE中,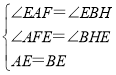 ,
,
∴△AFE≌△BHE(AAS),
∴BH=AF=4cm,
∴HC=16cm,
∵BC∥AD,
∴![]() ,即
,即![]() ,
,
∴CG=24,
则AC=AG+CG=30cm,
故答案为:30 cm.

练习册系列答案
相关题目