题目内容
 如图所示,梯形ABCD的对角线AC和BD相交于点O,OA=OD,AC=BD,则图中全等的三角形有
如图所示,梯形ABCD的对角线AC和BD相交于点O,OA=OD,AC=BD,则图中全等的三角形有
- A.1对
- B.2对
- C.3对
- D.4对
C
分析:根据等腰梯形的性质及全等三角形的判定可以得出图中有3对全等三角形,分别为:△ABO≌△DCO,△ABD≌△DCA,△ABC≌△DCB.
解答:∵OA=OD,AC=BD,
∴OC=OB,∠AOB=∠DOC,
∴△ABO≌△DCO(SAS),∠OBC=∠OCB,
∴梯形ABCD为等腰梯形,
∴AB=DC,∠BAD=∠CDA,
∴△ABC≌△DCB(SAS),
△ABD≌△DCA(SAS);
∴图中全等的三角形有3对.
故选C.
点评:本题主要考查了等腰梯形的性质及全等三角形的判定方法,常用的全等三角形的判定方法有SSS,SAS,AAS,ASA,HL等.
分析:根据等腰梯形的性质及全等三角形的判定可以得出图中有3对全等三角形,分别为:△ABO≌△DCO,△ABD≌△DCA,△ABC≌△DCB.
解答:∵OA=OD,AC=BD,
∴OC=OB,∠AOB=∠DOC,
∴△ABO≌△DCO(SAS),∠OBC=∠OCB,
∴梯形ABCD为等腰梯形,
∴AB=DC,∠BAD=∠CDA,
∴△ABC≌△DCB(SAS),
△ABD≌△DCA(SAS);
∴图中全等的三角形有3对.
故选C.
点评:本题主要考查了等腰梯形的性质及全等三角形的判定方法,常用的全等三角形的判定方法有SSS,SAS,AAS,ASA,HL等.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
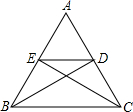 如图所示,在△ABC中,AB=AC,BD,CE分别为∠ABC,∠ACB的平分线.
如图所示,在△ABC中,AB=AC,BD,CE分别为∠ABC,∠ACB的平分线.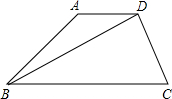 已知:如图所示,梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,BD=BC=4
已知:如图所示,梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,BD=BC=4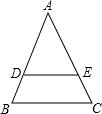 如图所示,在△ABC中,DE∥BC,△ADE和梯形DBCE的面积相等,则AD:DB=
如图所示,在△ABC中,DE∥BC,△ADE和梯形DBCE的面积相等,则AD:DB=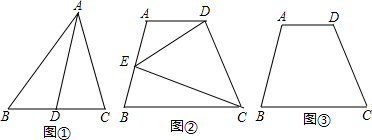
 梯形的边运动,设点P运动的路程为x,△ABP的面积为y,函数图象如图②所示,则△ABC面积为
梯形的边运动,设点P运动的路程为x,△ABP的面积为y,函数图象如图②所示,则△ABC面积为