题目内容
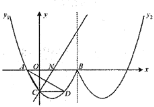
【题目】如图，二次函数
的图象经过点
，
，且与y轴交于点C．
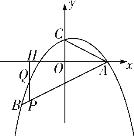
（1）求二次函数的解析式；
（2）证明：
（其中O是原点）；
（3）若P是线段
上的一个动点（不与A、B重合），过点P作y轴的平行线，分别交此二次函数图象及x轴于Q、H两点，试问：是否存在这样的点P，使
？若存在，请求出点P的坐标；若不存在，请说明理由．
【答案】(1)
；(2)存在,
与
【解析】
（1）解：∵点
、
在二次函数图象上，
∴
，
解得
，
∴二次函数解析式为；
（2）如图，过点B作
轴于点D，由（1）得
，
则在
中，
，
又在
中，
；
∵
，
∴
；
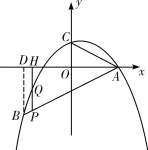
（3）存在，理由如下：
由点与可得直线
的解析式为
，
设
，
则
，
∴
，
．
要使
，
∴
．
当
时，
解得
，
（舍去），
∴
．
当
时，
解得
， （舍去），
∴
．
综上所述，存在满足条件的点P，它们是与．
练习册系列答案
相关题目
【题目】某公司购进一批受环境影响较大的商品，需要在特定的环境中才能保存，已知该商品成本y（元/件）与保存的时间第x（天）之间的关系满足y＝x2﹣4x+100，该商品售价p（元/件）与保存时间第x（天）之间满足一次函数关系，其对应数据如表：
x（天） | …… | 5 | 7 | …… |
p（元/件） | …… | 248 | 264 | …… |
（1）求商品的售价p（元/件）与保存时间第x（天）之间的函数关系式；
（2）求保存第几天时，该商品不赚也不亏；
（3）请你帮助该公司确定在哪一天卖出，每件商品能获得最大利润，此时每件商品的售价是多少？
