��Ŀ����
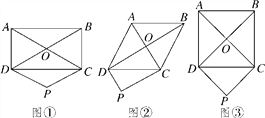
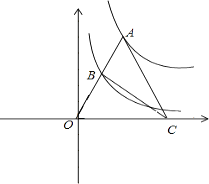
����Ŀ����ͼ��������OABC�ı�OA��OC���������ϣ���B������Ϊ����4��4������P�ӵ�A��������ÿ��1����λ���ȵ��ٶ���x�����O�˶�����Q�ӵ�Oͬʱ����������ͬ���ٶ���x����������˶����涨��P�����Oʱ����QҲֹͣ�˶�������BP����P����BP�Ĵ��ߣ������Qƽ����y���ֱ��l�ཻ�ڵ�D��BD��y�ύ�ڵ�E������PE�����P�˶���ʱ��Ϊt��s���� 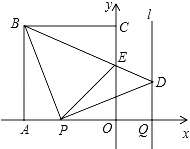
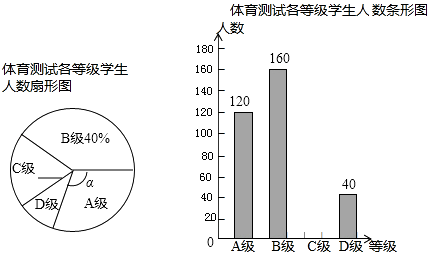
��1����PBD�Ķ���Ϊ �� ��D������Ϊ����t��ʾ����
��2����tΪ��ֵʱ����PBEΪ���������Σ�
��3��̽����POE�ܳ��Ƿ���ʱ��t�ı仯���仯�����仯��˵�����ɣ������䣬���������ֵ��
���𰸡�
��1���⣺45�㣻��t��t��
��2���⣺����PB=PE��
�ɡ�PAB�ա�DQP��PB=PD��
��ȻPB��PE��
���������Ӧ��ȥ��
����EB=EP��
���PBE=��BPE=45�㣮
���BEP=90�㣮
���PEO=90�㩁��BEC=��EBC��
�ڡ�POE�͡�ECB�У�
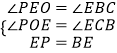
���POE�ա�ECB��AAS����
��OE=CB=OC��
���E���C�غϣ�EC=0����
���P���O�غϣ�PO=0����
�ߵ�B����4��4����
��AO=CO=4��
��ʱt=AP=AO=4��
����BP=BE��
��Rt��BAP��Rt��BCE��
![]()
��Rt��BAP��Rt��BCE��HL����
��AP=CE��
��AP=t��
��CE=t��
��PO=EO=4��t��
�ߡ�POE=90�㣬
��PE= ![]()
= ![]() ��4��t����
��4��t����
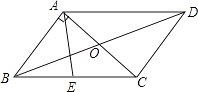
�ӳ�OA����F��ʹ��AF=CE������BF����ͼ2��ʾ��
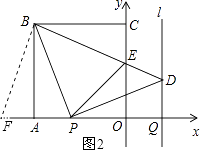
�ڡ�FAB�͡�ECB�У�
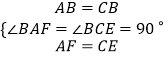
���FAB�ա�ECB��
��FB=EB����FBA=��EBC��
�ߡ�EBP=45�㣬��ABC=90�㣬
���ABP+��EBC=45�㣮
���FBP=��FBA+��ABP
=��EBC+��ABP=45�㣮
���FBP=��EBP��
�ڡ�FBP�͡�EBP�У�
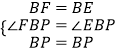
���FBP�ա�EBP��SAS����
��FP=EP��
��EP=FP=FA+AP
=CE+AP��
��EP=t+t=2t��
�� ![]() ��4��t��=2t��
��4��t��=2t��
��ã�t=4 ![]() ��4
��4
�൱tΪ4���4 ![]() ��4����ʱ����PBEΪ����������
��4����ʱ����PBEΪ����������
��3���⣺��EP=CE+AP��
��OP+PE+OE=OP+AP+CE+OE
=AO+CO
=4+4
=8��
���POE�ܳ��Ƕ�ֵ���ö�ֵΪ8
���������⣺��1����ͼ1�� 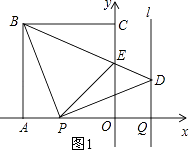
����ɵã�AP=OQ=1��t=t���룩
��AO=PQ��
���ı���OABC�������Σ�
��AO=AB=BC=OC��
��BAO=��AOC=��OCB=��ABC=90�㣮
��DP��BP��
���BPD=90�㣮
���BPA=90�㩁��DPQ=��PDQ��
��AO=PQ��AO=AB��
��AB=PQ��
�ڡ�BAP�͡�PQD�У�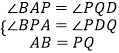
���BAP�ա�PQD��AAS����
��AP=QD��BP=PD��
�ߡ�BPD=90�㣬BP=PD��
���PBD=��PDB=45�㣮
��AP=t��
��DQ=t��
���D������t��t����
�ʴ�Ϊ��45�㣬��t��t����
��1����֤��BAP�ա�PQD���Ӷ��õ�DQ=AP=t���Ӷ����������PBD�Ķ����͵�D�����꣮��2�����ڡ�EBP=45�㣬��ͼ1����������Ϊ������һ������ͼ�Σ����õ�EP=AP+CE�����ڡ�PBE�ױ߲������ʷ�����������ۣ�������������ȫ�ȼ����ɶ���������⣬Ȼ������������ȡ�ᣬ����ȷ������Ҫ���tֵ����3���ɣ�2����֤�Ľ���EP=AP+CE�����õ���POE�ܳ�����AO+CO=8���Ӷ�������⣮

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�