Question

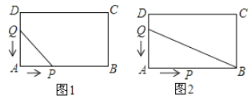
【题目】如图，在长方形中，10厘米，6厘米，点沿边从点开始向点以2厘米/秒的速度移动;点沿边从点开始向点以1厘米/秒的速度移动．如果同时出发，用 (秒)表示移动的时间．那么：

(1)如图1，用含的代数式表示和，若线段，求的值．

(2)如图2，在不考虑点的情况下，连接，用含t的代数式表示△QAB的面积．

(3)图2中，若△QAB的面积等于长方形的面积的，求的值．

Answer 1

【答案】（1）AP＝2t；AQ＝6－t；t＝2 （2）S△QAB＝﹣5t＋30 (0≤t≤6) （3）t＝2

【解析】

（1）根据P点、Q点的运动速度可得AP、AQ的长，再利用AP＝AQ列出方程，解方程即可；

（2）根据三角形的面积公式表示出△QAB的面积即可解答；

（3）在（2）的基础上，根据题意可列出关于t的方程，解方程即可．

解：（1）由题意知AP＝2t，AQ＝6－t，

当AP＝AQ时，2t＝6－t

解得：t＝2；

故答案为：2t；6－2t；t＝2

（2）由题意可知：S△QAB＝AB·AQ＝×10×(6－t) ＝﹣5t＋30 (0≤t≤6);

（3）由已知可得：S△QAB＝S长方形ABCD，

则﹣5t＋30＝×10×6

解得：t＝2

答：若△QAB的面积等于长方形的面积的， 的值为2．