题目内容
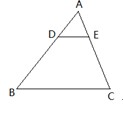
如图,在边长为9的正三角形ABC中,BD=3,∠ADE=60°,则AE的长为_________.
7
解析试题分析:∵△ABC是等边三角形,
∴∠B=∠C=60°,AB=BC;
∴CD=BC﹣BD=9﹣3=6;
∴∠BAD+∠ADB=120°
∵∠ADE=60°,
∴∠ADB+∠EDC=120°,
∴∠DAB=∠EDC,
又∵∠B=∠C=60°,
∴△ABD∽△DCE,
则 =
=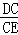 ,
,
即 =
=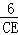 ,
,
解得:CE=2,
故AE=AC﹣CE=9﹣2=7.
故答案为:7.
考点:1.相似三角形的判定与性质;2.等边三角形的性质.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目

 ,则
,则 的值为__________.
的值为__________.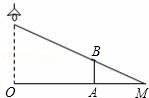
 ∥
∥ ∥
∥ ,
, ,
,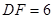 ,
, ,则
,则 .
.
 ∥
∥ ,
,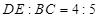 ,则
,则 .
.

 ,若△AEF的面积为2,则四边形EBCF的面积为 .
,若△AEF的面积为2,则四边形EBCF的面积为 .