题目内容
如图,△ABC是等边三角形,且AB∥CE.
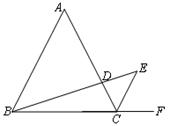
(1) 求证:△ABD∽△CED;
(2) 若AB=6,AD=2CD,
①求E到BC的距离EH的长.
② 求BE的长
【答案】
(1)相似三角形角度的相等即可(2)EH=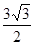 (2)BE的长为
(2)BE的长为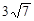
【解析】
试题分析:由题意可知,因为AB∥CE,所以
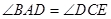
同时,根据对顶角相等,可以知道
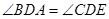
所以△ABD∽△CED
(2)由上知△ABD∽△CED
所以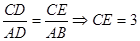
同时,根据△ABC是等边三角形,所以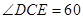
所以在直角三角形ECH中,EH=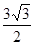
(3)在直角三角形BEH中,因为EH= 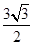 ,
, 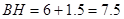
所以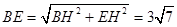
考点:全等三角形的性质和判定
点评:解答本题的关键是熟练掌握判定两个三角形全等的一般方法:SSS、SAS、ASA、AAS、HL,注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
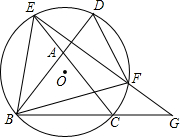 ∥AC,EF的延长线交BC的延长线于点G.
∥AC,EF的延长线交BC的延长线于点G. 9、如图,△ABC是等边三角形,过AB边上一点D作BC的平行线交AC于E,则△ADE的三个内角
9、如图,△ABC是等边三角形,过AB边上一点D作BC的平行线交AC于E,则△ADE的三个内角 如图,△ABC是等边三角形,AB=4cm,则BC边上的高AD等于
如图,△ABC是等边三角形,AB=4cm,则BC边上的高AD等于 如图,△ABC是等边三角形,D为BC边上的点,∠BAD=15°,将△ABD绕点A点逆时针方向旋转后到达△ACE的位置,那么旋转角的度数是
如图,△ABC是等边三角形,D为BC边上的点,∠BAD=15°,将△ABD绕点A点逆时针方向旋转后到达△ACE的位置,那么旋转角的度数是 如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.
如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.