题目内容
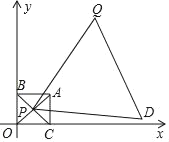
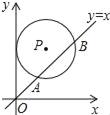
【题目】如图,在平面直角坐标系中,⊙P的圆心是(3,a)(a>3),⊙P与y轴相切,函数y=x的图象被⊙P截得的弦AB的长为2![]() ,则a的值是_____.
,则a的值是_____.
【答案】2![]() +3.
+3.
【解析】
作PH⊥y轴于H,PC⊥AB于C,作PE⊥x轴于E交AB于D,如图,先根据切线的性质得PH=2,即⊙P的半径为2,再根据垂径定理,由PC⊥AB得到![]() ,接着在Rt△BPC中利用勾股定理可计算出PC=1,由直线y=x为第一、三象限的角平分线得到∠DOE=45°,则∠ODE=45°,DE=OE=2,然后判断△PCD为等腰直角三角形得到
,接着在Rt△BPC中利用勾股定理可计算出PC=1,由直线y=x为第一、三象限的角平分线得到∠DOE=45°,则∠ODE=45°,DE=OE=2,然后判断△PCD为等腰直角三角形得到![]() 所以
所以![]() 即
即![]()
解:作PH⊥y轴于H,PC⊥AB于C,作PE⊥x轴于E交AB于D,如图,
∵⊙P与y轴相切,
∴PH=2,即⊙P的半径为2,
∵PC⊥AB,
∴![]()
在Rt△BPC中,![]()
∵直线y=x为第一、三象限的角平分线,
∴∠DOE=45°,
∴∠ODE=45°,DE=OE=3,
∴∠PDC=45°,
∴![]()
∴![]()
故答案为:![]()


练习册系列答案
相关题目