题目内容
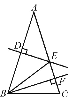
【题目】如图，平行四边形ABCD中，点E、F分别是AD、AB的中点，EF交AC于点G，那么AG：GC的值为（ ）
A.1：2
B.1：3
C.1：4
D.2：3
【答案】B
【解析】连接BD，与AC相交于O，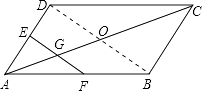 
∵点E、F分别是AD、AB的中点，
∴EF是△ABD的中位线，
∴EF∥DB，且EF= 
DB，
∴△AEF∽△ADB， 
= 
，
∴ 
= = ，
∴ = ，即G为AO的中点，
∴AG=GO，又OA=OC，
∴AG：GC=1：3．
所以答案是：B．
【考点精析】解答此题的关键在于理解三角形中位线定理的相关知识，掌握连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半，以及对平行四边形的性质的理解，了解平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分．
练习册系列答案
相关题目
